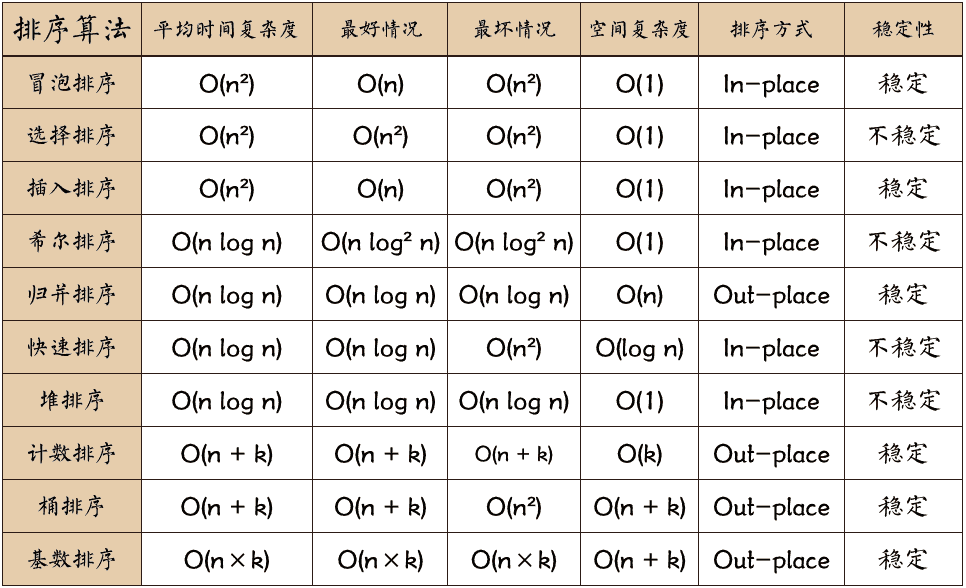
常见排序算法总结
AI-摘要
切换
小郭 GPT
AI初始化中...
介绍自己
生成本文简介
推荐相关文章
前往主页
前往tianli博客
本文最后更新于 2024-02-09,文章发布日期超过365天,内容可能已经过时。
冒泡排序
// 冒泡排序
// 时间复杂度:O(n^2)
// 空间复杂度:O(1)
// 稳定性:稳定
// 可以用于链表、数组,这里以数组为例
#include <stdio.h>
void BubbleSort(int a[], int n);
int main()
{
int a[10] = {5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
BubbleSort(a, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
return 0;
}
void BubbleSort(int a[], int n)
{
int i, j, temp;
for (i = 0; i < n - 1; i++) // n个数排序,只用进行n-1趟
{
int falg = 0; // 标记,如果一趟比较下来没有发生交换,则说明已经排好序了
for (j = 0; j < n - 1 - i; j++) // 从第1位开始比较直到最后一个尚未归位的数,每比较一次就把最大的数冒泡到最后
{
if (a[j] > a[j + 1]) // 把小的数交换到后面
{
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
falg = 1;
}
}
if (falg == 0) // 一趟比较下来没有发生交换,说明已经排好序了,直接跳出循环
{
break;
}
}
}选择排序
// 简单选择排序
// 时间复杂度:O(n^2)
// 空间复杂度:O(1)
// 稳定性:不稳定
// 可以用于链表、数组,这里以数组为例
#include <stdio.h>
void SelectionSort(int a[], int n);
int main()
{
int a[10] = {5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
SelectionSort(a, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
return 0;
}
void SelectionSort(int a[], int n){
for(int i=0;i<n-1;i++){
int min = i;
for(int j=i+1;j<n;j++){
if(a[j]<a[min]){
min = j;
}
}
if(min!=i){
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
}
插入排序
// 插入排序
// 这里以数组从小到大排序为例,链表同理,不能使用折半插入优化算法
// 时间复杂度:O(n^2)
// 空间复杂度:O(1)
// 稳定性:稳定
#include <stdio.h>
void InsertSort1(int a[], int n);
void InsertSort2(int a[], int n);
void InsertSort3(int a[], int n);
int main()
{
int a[10] = {5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
InsertSort1(a, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
int b[11] = {NULL, 5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
InsertSort2(b, 10);
for (int i = 1; i < 11; i++)
{
printf("%d ", b[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
int c[11] = {NULL, 5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
InsertSort3(c, 10);
for (int i = 1; i < 11; i++)
{
printf("%d ", c[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
return 0;
}
// 插入排序(不带哨兵)
// 从小到大排序
void InsertSort1(int a[], int n)
{
for (int i = 1; i < n; i++)
{
if (a[i] < a[i - 1])
{
int temp = a[i], j;
for (j = i - 1; j >= 0 && a[j] > temp; j--)
{
a[j + 1] = a[j];
}
a[j + 1] = temp;
}
}
}
// 插入排序(带哨兵)
// 从小到大排序
void InsertSort2(int a[], int n)
{
for (int i = 2; i <= n; i++)
{
if (a[i] < a[i - 1])
{
// 哨兵,启动!
a[0] = a[i];
int j;
for (j = i - 1; a[0] < a[j]; j--)
{
// 可以看到循环中少了大于0的判断
a[j + 1] = a[j];
}
a[j + 1] = a[0];
}
}
}
// 插入排序(折半插入优化)
// 从小到大排序
void InsertSort3(int a[], int n)
{
for (int i = 2; i <= n; i++)
{
if (a[i] < a[i - 1])
{
// 哨兵,启动!
a[0] = a[i];
int low = 1, high = i - 1;
while (low <= high)
{
int mid = (low + high) / 2;
if (a[mid] > a[0])
{
high = mid - 1;
}
else
{
low = mid + 1;
}
}
for (int j = i - 1; j >= high + 1; j--)
{
a[j + 1] = a[j];
}
a[high + 1] = a[0];
}
}
}快速排序
// 快速排序
// 时间复杂度:最好O(nlogn),最坏O(n^2),平均O(nlogn)
// 空间复杂度:最好O(logn),最坏O(n),平均O(logn)
// 稳定性:不稳定
// 可以用于链表、数组,这里以数组为例
// 快速排序是所有内部排序算法中平均性能最优的排序算法
#include <stdio.h>
void QuickSort(int a[], int n);
int main()
{
int a[10] = {5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
QuickSort(a, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
return 0;
}
void QuickSort(int a[], int n)
{
if (n <= 1)
{
return;
}
// 选取第一个元素作为基准
int pivot = a[0];
int low = 0;
int high = n - 1;
while (low < high)
{
// 从右向左找到第一个小于基准的元素
while (low < high && a[high] >= pivot)
{
high--;
}
// 将小于基准的元素放到左边
a[low] = a[high];
// 从左向右找到第一个大于基准的元素
while (low < high && a[low] <= pivot)
{
low++;
}
// 将大于基准的元素放到右边
a[high] = a[low];
}
// 循环结束时,low == high,将基准放到该位置
a[low] = pivot;
// 递归处理左右两边
QuickSort(a, low);
QuickSort(a + low + 1, n - low - 1);
}堆排序
// 堆排序
// 这里以数组从小到大排序为例,链表同理
// 建立初始堆的时间复杂度为O(n)
// 时间复杂度:O(nlogn)
// 空间复杂度:O(1)
// 稳定性:不稳定
#include <stdio.h>
void HeapSort(int a[], int n);
int main()
{
int a[11] = {NULL,5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
HeapSort(a, 10);
for (int i = 1; i <= 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
return 0;
}
void HeapSort(int a[], int n)
{
// 递归出口
if (n == 1)
return;
// 建立大根堆
for (int i = n / 2 ; i >= 0; i--)
{
int temp = i;
// 从最后一个非叶子节点开始调整,将其放入哨兵位置
a[0]=a[temp];
for(int j=2*temp;j<=n;j*=2)
{
// 选出左右孩子中较大的一个,这里使用小于n是为了使其有右孩子
if(j<n&&a[j]<a[j+1])
j++;
// 如果根节点大于左右孩子中较大的一个,则不用交换
if(a[0]>=a[j])
break;
else
{
a[temp]=a[j];
temp=j;
// 交换后,i指向被交换的孩子节点,继续向下调整
}
}
a[temp]=a[0];
}
// 将根节点与最后一个节点交换,然后将剩余的n-1个节点重新调整为大根堆
int temp = a[1];
a[1] = a[n];
a[n] = temp;
HeapSort(a, n - 1);
// 都写到在这里了,其实仔细看看就可以发现没必要使用递归,直接用循环就可以,这里就不改了
}归并排序
// 归并排序
// 内部排序中一般采用二路归并,执行多次后完成对一个数组的排序
// 稳定性:稳定
// 时间复杂度:O(nlogn)
// 空间复杂度:O(n)
#include <stdio.h>
#include <stdlib.h>
// 二路归并排序
int* MergeSort2(int a[], int b[], int na, int nb);
// 四路归并排序
int* MergeSort4(int a[], int b[], int c[], int d[], int na, int nb, int nc, int nd);
int main()
{
// 准备两个有序序列
int a[10] = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
int b[10] = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20};
// 合并两个有序序列
int* c = MergeSort2(a, b, 10, 10);
// 打印合并后的序列
for (int i = 0; i < 20; i++)
{
printf("%d ", c[i]);
}
printf("\n");
// 准备四个有序序列
int a1[10] = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
int b1[10] = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20};
int c1[10] = {21, 23, 25, 27, 29, 31, 33, 35, 37, 39};
int d1[10] = {22, 24, 26, 28, 30, 32, 34, 36, 38, 40};
// 合并四个有序序列
int* e = MergeSort4(a1, b1, c1, d1, 10, 10, 10, 10);
// 打印合并后的序列
for (int i = 0; i < 40; i++)
{
printf("%d ", e[i]);
}
printf("\n");
return 0;
}
int* MergeSort2(int a[], int b[], int na, int nb){
// 申请一个新的数组,用于存放合并后的序列
int* c = (int*)malloc(sizeof(int) * (na + nb));
// 两个序列的下标
int i = 0, j = 0;
// 合并后序列的下标
int k = 0;
// 两个序列都没有遍历完时,比较两个序列的元素,将较小的元素放入合并后的序列
while (i < na && j < nb)
{
if (a[i] < b[j])
{
c[k++] = a[i++];
}
else
{
c[k++] = b[j++];
}
}
// 如果a序列还没有遍历完,将剩余的元素放入合并后的序列
while (i < na)
{
c[k++] = a[i++];
}
// 如果b序列还没有遍历完,将剩余的元素放入合并后的序列
while (j < nb)
{
c[k++] = b[j++];
}
return c;
}
int* MergeSort4(int a[], int b[], int c[], int d[], int na, int nb, int nc, int nd){
// 申请一个新的数组,用于存放合并后的序列
int* e = (int*)malloc(sizeof(int) * (na + nb + nc + nd));
// 四个序列的下标
int i = 0, j = 0, k = 0, l = 0;
// 合并后序列的下标
int m = 0;
// 四个序列都没有遍历完时,比较四个序列的元素,将较小的元素放入合并后的序列
while (i < na && j < nb && k < nc && l < nd)
{
if (a[i] < b[j] && a[i] < c[k] && a[i] < d[l])
{
e[m++] = a[i++];
}
else if (b[j] < a[i] && b[j] < c[k] && b[j] < d[l])
{
e[m++] = b[j++];
}
else if (c[k] < a[i] && c[k] < b[j] && c[k] < d[l])
{
e[m++] = c[k++];
}
else
{
e[m++] = d[l++];
}
}
// 如果a序列还没有遍历完,将剩余的元素放入合并后的序列
while (i < na)
{
e[m++] = a[i++];
}
// 如果b序列还没有遍历完,将剩余的元素放入合并后的序列
while (j < nb)
{
e[m++] = b[j++];
}
// 如果c序列还没有遍历完,将剩余的元素放入合并后的序列
while (k < nc)
{
e[m++] = c[k++];
}
// 如果d序列还没有遍历完,将剩余的元素放入合并后的序列
while (l < nd)
{
e[m++] = d[l++];
}
return e;
}基数排序
// 基数排序
// 基数排序通常基于链表实现,这里为了易于理解,主要使用数组实现,辅助队列使用链表实现
// 时间复杂度:O(d(n+r)), d为关键字的位数,r为关键字的基数, n为关键字个数
// 空间复杂度:O(r), r为关键字的基数
// 稳定性:稳定
// 思路可以进一步拓展,也不一定要单独位数,其实就是一个权重的比较,举例学生生日,按照年月日排序,先按照日排序,再按照月排序,最后按照年排序
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define MAX 100
// 基数排序使用链表存储数据
typedef struct node {
int data;
struct node *next;
} Node;
// 链式队列
typedef struct {
Node *head;
Node *tail;
} List;
// 初始化链表
void initList(List *list) {
list->head = NULL;
list->tail = NULL;
}
// 链表尾部插入
void insertList(List *list, int data) {
Node *node = (Node *)malloc(sizeof(Node));
node->data = data;
node->next = NULL;
if (list->head == NULL) {
list->head = node;
list->tail = node;
} else {
list->tail->next = node;
list->tail = node;
}
}
// 链表头部删除
int deleteList(List *list) {
if (list->head == NULL) {
return -1;
}
Node *node = list->head;
int data = node->data;
list->head = node->next;
free(node);
return data;
}
// 打印链表
void printList(List *list) {
Node *node = list->head;
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
printf("\n");
}
// 基数排序
void radixSort(int *arr, int n) {
// 10个链表,分别存储0-9的数据
List lists[10];
for (int i = 0; i < 10; i++) {
initList(&lists[i]);
}
// 最大值
int max = arr[0];
// 最大值的位数
int maxDigit = 1;
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
while (max / 10 > 0) {
maxDigit++;
max /= 10;
}
// 从低位到高位,依次比较
for (int i = 0; i < maxDigit; i++) {
// 将数据放入对应的链表中
for (int j = 0; j < n; j++) {
int index = (arr[j] / (int)pow(10, i)) % 10;
insertList(&lists[index], arr[j]);
}
// 将链表中的数据取出来
int index = 0;
for (int j = 0; j < 10; j++) {
while (lists[j].head != NULL) {
arr[index++] = deleteList(&lists[j]);
}
}
}
}
int main() {
int arr[MAX];
int n;
printf("请输入数据个数:");
scanf("%d", &n);
printf("请输入%d个数据:", n);
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
radixSort(arr, n);
printf("排序后的结果:");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}希尔排序
// 希尔排序
// 只可以基于顺序表实现,不可以基于链表实现
// 时间复杂度:和增量序列d,d2,d3...的选择有关,目前无法用数学手段证明确切的时间复杂度最坏时间复杂度为O(n2),当n在某个范围内时,可达O(n1.3)
// 空间复杂度:O(1)
// 稳定性:不稳定
#include <stdio.h>
void ShellSort(int a[], int n);
int main()
{
int a[11] = {NULL, 5, 1, 7, 2, 5, 9, 8, 0, 7, 3};
// 第一个空位为哨兵位
ShellSort(a, 10);
for (int i = 1; i <= 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
// 结果:0 1 2 3 5 5 7 7 8 9
return 0;
}
void ShellSort(int a[], int n)
{
int i, j, d;
for (d = n / 2; d >= 1; d = d / 2) // 增量序列
{
for (i = d + 1; i <= n; i++)
{
if (a[i] < a[i - d])
{
a[0] = a[i];
for (j = i - d; j > 0 && a[0] < a[j]; j -= d)
{
a[j + d] = a[j];
}
a[j + d] = a[0];
}
}
}
}- 感谢你赐予我前进的力量
赞赏者名单
因为你们的支持让我意识到写文章的价值🙏
本文是原创文章,采用 CC BY-NC-ND 4.0 协议,完整转载请注明来自 郭同学的笔记本
评论
匿名评论
隐私政策
你无需删除空行,直接评论以获取最佳展示效果



