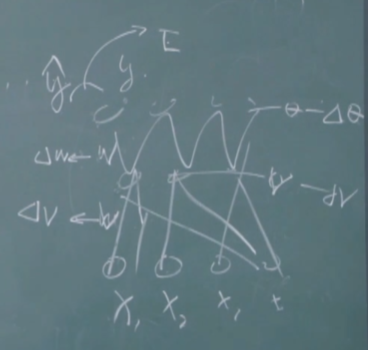机器学习理论入门-西瓜书

该文章数学公式较多，Latex渲染失败刷新页面即可

• 测试公式：​ 4x^{2}+\sqrt{y}=\frac{z}{3}
• 若显示 4x^{2}+\sqrt{y}=\frac{z}{3}即为渲染失败，再次刷新页面即可正常显示

写在前面

周志华老师的《机器学习》（西瓜书）是机器学习领域的经典入门教材之一，博主花费了一个月时间粗读，并进行了知识梳理以及相关公式推导，诞生了此文。文章目前涵盖了机器学习基础知识、线性模型、神经网络、支持向量机以及计算学习理论的内容，剩余的其他知识点也在持续缓慢更新中。这篇文章精简了复杂难懂的理论、公式，对每一个抽象的定义都附上了个人通俗理解，并对难点重点给出了博主推荐的讲解链接。如果你急需投身项目实践，又缺乏相应的理论基础，这篇文章可以作为你的快速入门首选。

✨所需要的前置知识：概率论，高数，线代，数论，数据结构

西瓜书-图书资源下载

推荐配套辅导书籍：南瓜书（对西瓜书中的每一个公式给出它的零基础推理）

画了个一三五六章的结构图，其他章节有时间再慢慢补着画完吧👇

第一章 绪论

1.1 思维启发

机器学习就是一个算法吗？

科学、技术、工程、应用的区别？

• 科学解决的是是什么与为什么的问题
• 技术解决的是怎么做
• 工程解决的是怎样做的多快好省
• 应用就是字面上的意思

周志华老师在课程中举了一个菜刀的例子，通俗易懂

西瓜书面向的更多的是科学与技术层面的

1.2 机器学习

机器学习的经典定义：利用经验改善系统自身的性能

机器学习的经验->数据

随着该领域的发展，目前主要研究智能数据分析的理论和方法，并已成为智能数据分析技术的源泉之一

大数据时代中，目前阶段大数据≠大价值，因此有极大的数据处理的需求

1.3 典型的机器学习过程

以西瓜的色泽、根蒂、敲声这三种数据，来判断一个西瓜是否为一个好瓜

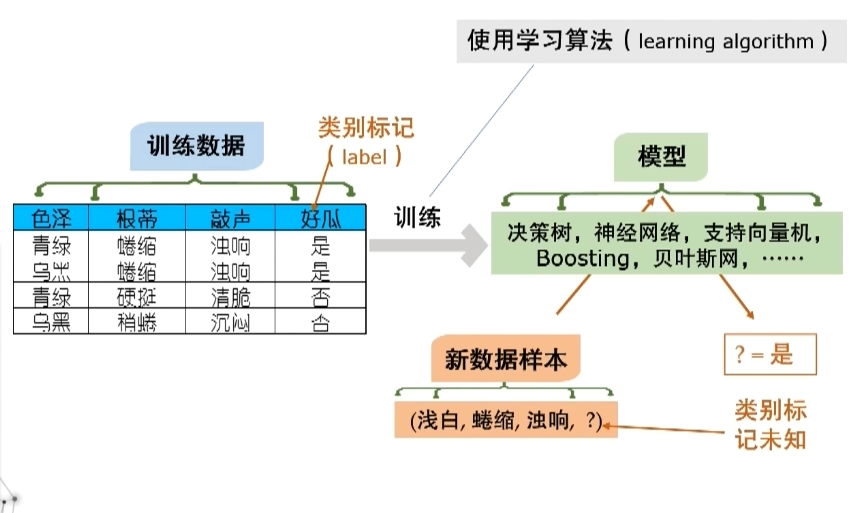
在这本书中，不做具体的区分，从数据里面产生出来的能够处理未来事件的东西都叫做模型

1.4 机器学习理论

机器学习有坚实的理论基础

最重要的理论模型：PAC（Probably Approximately Correct，概率近似正确）

• ​P(|f(\boldsymbol{x})-y|\leq\epsilon)\geq1-\delta （像概率论切比雪夫不等式哈哈哈）

当我们的知识已经不能给出一个精确的结果的时候，就需要机器学习来从数据中得出答案的估计

什么是​P?=NP问题？

P与NP问题是计算机科学中的一个重要问题，涉及到计算问题的可解性和复杂性。

P问题是指在多项式时间内可以有效解决的问题集合。换句话说，如果一个问题属于P，那么存在一个多项式时间算法能够解决这个问题。

NP问题则是指在多项式时间内可以验证解的问题集合。如果一个问题的解可以在多项式时间内被验证，那么它属于NP。

P与NP问题的关系是一个未解决的问题，即P与NP问题：它们之间是否存在相等关系，即P是否等于NP。这个问题的正面回答意味着所有可以在多项式时间内验证的问题都可以在多项式时间内解决，从而许多在实际应用中很难解决的问题可以被有效地解决。

P：算起来很快的问题

NP：算起来不一定快，但对于任何答案我们都可以快速的验证这个答案对不对

1.5 基本术语

以章节1.3中的表格为例

• 数据集；训练，测试

  测试是把模型拿来用，测试数据与训练数据是分开的

• 示例(instance)，样例(example)

  示例指给出的西瓜的各项属性

  样例是有结果的，告诉你这个西瓜好不好

• 样本(sample)

  比较含糊，根据上下文

• 属性(attribute)，特征(feature);属性值

  颜色是青绿色，这个颜色就是一个属性

  属性值就是在这个属性上的取值

• 属性空间，样本空间，输入空间

  由各属性组成的一个向量空间

• 特征向量（featurevector)

• 标记空间，输出空间

• 假设（hypothesis)，真相(ground-truth)，学习器（learner）

• 分类，回归

  分类问题是机器学习研究的最基础问题，特别是二分类，一切分类都可以以二分类为基础

• 二分类，多分类，正类，反类

• 监督学习（supervisedlearning），无监督学习（unsupervisedlearning)

  对于1.3表格，有最右面的部分的就是监督学习，没有的就是无监督（是否有期望结果）

  显而易见，无监督学习无法判断西瓜的好坏，但是可以分类等

• 未见样本（unseeninstance）

  为什么能处理没有见过的数据呢，因为我们有一个基本假设，就是未知数据与原来的数据来自同一个分布

• 未知“分布“

• 独立同分布（i.i.d.）

  所有数据都是从一个地方来的，每一个样本都是独立的，同分布的

  现实任务真的是独立同分布吗？这方面的研究是机器学习最前沿的，作为入门不需要了解，默认独立同分布

• 泛化（generalization）

  学到的模型处理新数据的能力，越能处理新数据，泛化能力越强

  ​P(|f(\boldsymbol{x})-y|\leq\epsilon)\geq1-\delta

  其实就是在求​|f(\boldsymbol{x})-y|\leq\epsilon 中你这个​\epsilon 能做到多小，如果​\epsilon 是0.5，那别做优化了，再做也跟随机猜测没有区别

• 特化

1.6 归纳偏好

机器学习算法在学习过程中对某种类型假设的偏好

当出现这种情况是，选择A还是选择B，叫做算法的偏好

一般原则：奥卡姆剃刀(Occam's razor)

奥卡姆剃刀：若非必要，勿增实体

当多种理论都可以解释我们的实体，我们选择最简单的，机器学习中同样如从，选择最简单的模型

但是一定选择简单的就好吗？

​\begin{aligned}y&=ax^{2}+bx+c\\y&=ax^{3}+c\end{aligned}

这是两个曲线方程，我可以说是二阶的更简单，也可以说三阶参数少更简单，所以判断哪个简单不是一个简单的问题，所以这就导致机器学习有那么多算法，每个算法所选择的偏好不同

学习算法的归纳偏好是否与问题本身匹配大多数时候直接决定了算法能否取得好的性能！

1.8 NFL定理

NFL定理：一个算法a若在某些问题上比另一个算法，好，必存在另一些问题比a好

这个道理遍布于我们从小学到现在各个学科的方方面面，我认为这种”保持平衡“的定理很具有哲学意义

第二章 模型评估与选择

2.1 泛化能力

搞清楚到底要什么

模型给出的结果是否是所需的

但现在问题在于，我们手上没有unseeninstance

2.2 过拟合和欠拟合

泛化误差：在“未来”样本上的误差

经验误差：在训练集上的误差，亦称“训练误差”

经验误差是不是越小越好？

• 不是，因为会出现过拟合

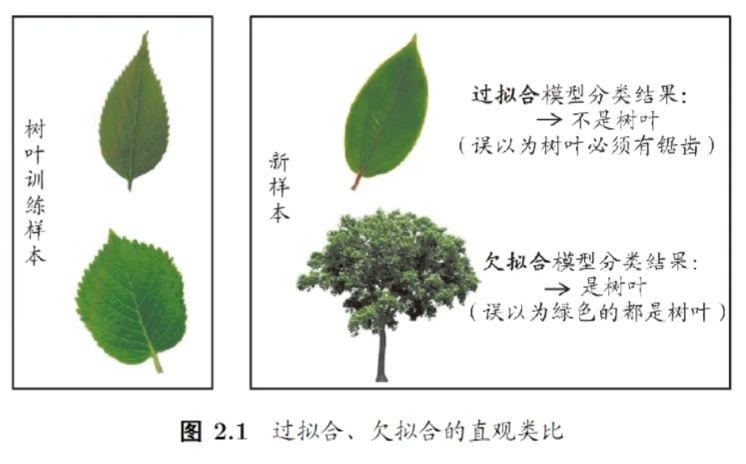
所以误差与拟合程度的图像通常是一个U型曲线（通常伴随着的是训练误差一直在下降）

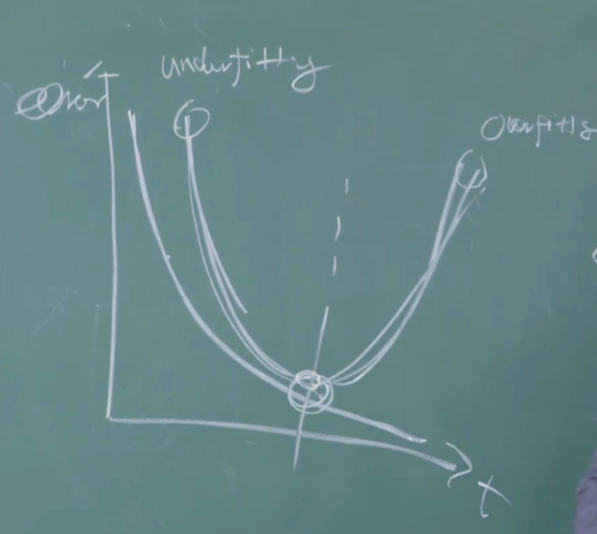
各种各样的算法都是在和这件事作斗争，是怎样来缓解overfighting的，思考这种缓解的技术在什么时候会失效

2.3 三大问题

三个关键问题：

• 如何获得测试结果？评估方法
• 如何评估性能优劣？性能度量
• 如何判断实质差别？比较检验

2.4 评估方法

关键：怎样获得“测试集”（test set）

测试集应该与训练集“互斥”

但是手上只有一个数据集怎么办，常见生成测试集的方法：

• 留出法(hold-out)

  将给出的数据留出一部分用于测试

  • 保持数据分布一致性（例如：分层采样（根据类别均匀的分布数据））
  • 多次重复划分（例如：100次随机划分）
  • 测试集不能太大、不能太小（例如：1/5~1/3）

  用此方法得到合适的模型后还要怎么做呢？周志华老师巧妙讲解（算出M80再求M100，划分只是起到了一个选择的作用）

• 交叉验证法（crossvalidation)

  K-折交叉验证法，解决留出法随机划分取不到某些数据的缺点

  

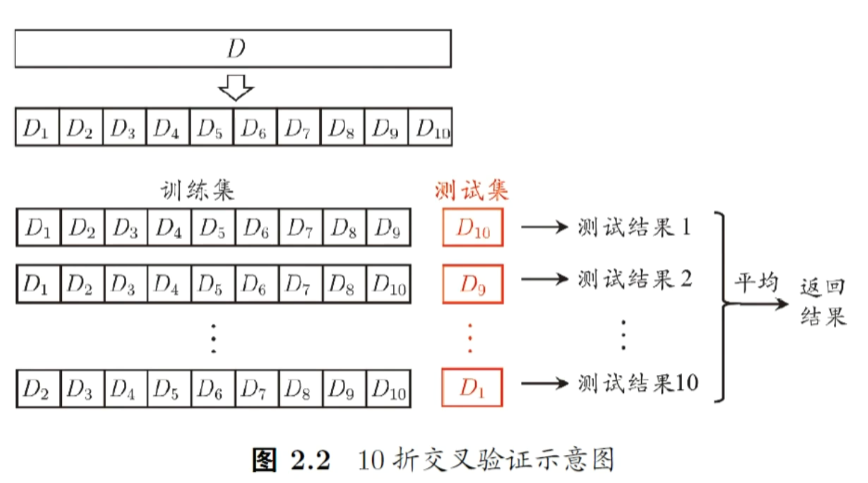
  即使这样了，还会存在一个问题，就是切分的划分也会存在扰动，测试集大小与训练集也可以继续变化，即10*10次实验

  为什么还要在每次的划分上跑一边，难道不是对于100个数据来说99+1的组合就是最准确的了吗？老师举了一个抽男生与女生的例子很形象

  若k=m，则得到“留一法(leave-one-out, LOO)

  答案：不是最准的，这样做的话每次做的都只有一个样本，虽然得到的模型与最终的​M_{100}很接近了，但是测试每次都是用的是一个样本，测试可能会有偏差。留的样本与用于测试的样本数量，对于模型准确性的影响本身就是一个矛盾的事情

• 自助法(bootstrap)

  自助法就是用于解决交叉验证法的矛盾问题的

  基于“自助采样”(bootstrap sampling)，亦称“有放回采样”、“可重复采样“

  放回采样，要100的模型就摸100个，但是由于是放回摸，所以会有没有摸到的球可以用来做测试集

  约有36.8%的样本不出现

  ​\lim_{m\to\infty}\left(1-\frac{1}{m}\right)^m=\frac{1}{e}\approx0.368

  “包外估计”(out-of-bag estimation)

  缺陷：改变了包外数据的分布，数据分布有所改变

2.5 调参与验证集

算法的参数：一般由人工设定，亦称“超参数”

模型的参数：一般由学习确定

调参过程相似：先产生若干模型，然后基于某种评估方法进行选择

参数调得好不好对性能往往对最终性能有关键影响

区别：训练集VS.测试集VS.验证集(validation set)

• 验证集就是专门用来调参数的数据集
• 测试集一定是要在训练过程中没有用到的，而验证机是训练的一部分
• 算法参数选定后，要用“训练集+验证集”重新训练最终模型

2.6 性能度量

性能度量(performancemeasure)是衡量模型泛化能力的评价标准，反映了任务需求

使用不同的性能度量往往会导致不同的评判结果

什么样的模型是“好”的，不仅取决于算法和数据，还取决于任务需求

回归(regression)任务常用均方误差：​E(f;D)=\frac{1}{m}\sum_{i=1}^{m}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2}

错误率：​E(f;D)=\frac1m\sum_{i=1}^m\mathbb{I}\left(f\left(\boldsymbol{x}_i\right)\neq y_i\right)

精度：​\begin{array}{rcl}\operatorname{acc}(f;D)&=&\dfrac{1}{m}\sum\limits_{i=1}^{m}\mathbb{I}\left(f\left(x_i\right)=y_i\right)\\&=&1-E\left(f;D\right).\end{array}

查准率VS.查全率

好像概率论哈哈哈哈

• 查准率（precision）：​P=\frac{TP}{TP+FP}

• 查全率：​R=\frac{TP}{TP+FN}

  对于这两个概念清晰明了的解释

将这两个合在一起，变成：

• F1度量： ​\begin{aligned}F1& =\frac{2\times P\times R}{P+R} \\&=\frac{2\times TP}{\text{样例总数}+TP-TN}\end{aligned}

  看着不好记，实际上就是调和平均​\frac1{F1}=\frac12\cdot\left(\frac1P+\frac1R\right)的化简

  为什么不是直接相加除以二而是使用调和？可以使较小的值不容易被忽视掉

• 若对查准率/查全率有不同偏好：​F_\beta=\frac{(1+\beta^2)\times P\times R}{(\beta^2\times P)+R}

  即​\frac1{F_\beta}=\frac1{1+\beta^2}\cdot\left(\frac1P+\frac{\beta^2}R\right)式子的化简，加上了权重

  β>1时查全率有更大影响；β<1时查准率有更大影响

2.7 比较检验

在某种度量下取得评估结果后，是否可以直接比较以评判优劣？

• 测试性能不等于泛化性能
• 测试性能随着测试集的变化而变化
• 很多机器学习算法本身有一定的随机性

机器学习————>概率近似正确

统计假设检验（hypothesis test）为学习器性能比较提供了重要依据

概率论知识

• 两学习器比较
  • 交叉验证 t检验 (基于成对t检验)
    • k折交叉验证；5x2交叉验证
  • McNemar检验（基于列联表，卡方检验)

第三章 线性模型

LinearRegression

3.1 线性回归

考虑线性问题会有一个直观的几何印象

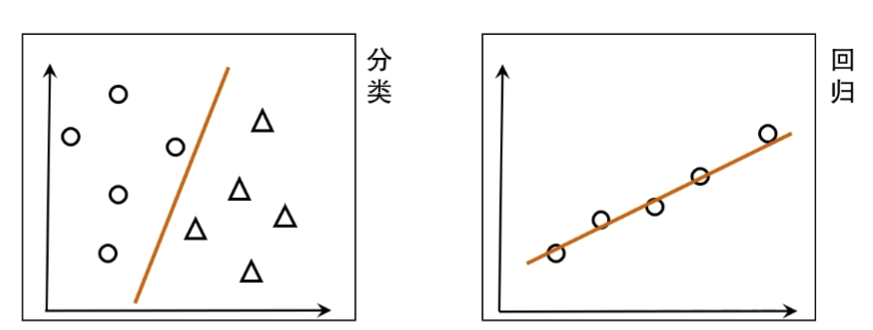
线性模型（linearmodel)试图学得一个通过属性的线性组合来进行预测的函数

• ​f(x)=w_1x_1+w_2x_2+\ldots+w_dx_d+b

• 向量属性：​f(x)=w^\mathrm{T}x+b

  T表示向量的转转置，向量的转置是指将一个列向量变成一个行向量，或将一个行向量变成一个列向量。在线性代数中，向量通常表示为一个包含多个数值的有序列表。例如，一个列向量可以表示为：​\mathbf{v}=\begin{bmatrix}v_1\\v_2\\\vdots\\v_n\end{bmatrix}

  其中 ​v_1,v_2,\ldots,v_n是向量的元素。通过转置操作，可以将列向量转换为行向量，或将行向量转换为列向量。

  对于上述的列向量 v，其转置表示为：​\mathbf{v}^T=[v_1,v_2,\ldots,v_n]

  在转置操作中，列向量的转置是一个行向量，而行向量的转置是一个列向量。转置并不改变向量中元素的顺序，只是改变了向量的排列方式

​\begin{aligned}f(x_i)&=wx_i+b\text{ 使得 }f(x_i)\simeq y_i\end{aligned}

关键：把离散的东西转成连续的东西的一个变换

例如：高、中、低，高可以是1，中0.5，低0

可以把离散的属性变成一个K位编码、K维向量

令均方误差最小化，有

​\begin{aligned}(w^*,b^*)& =\arg\min_{(w,b)}\sum_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2} \\&\begin{aligned}&=\arg\min_{(w,b)}\sum_{i=1}^m\left(y_i-wx_i-b\right)^2\end{aligned}\end{aligned}

对​E_{(w,b)}=\sum_{i=1}^m\left(y_i-wx_i-b\right)^2进行最小二乘参数估计

3.2 最小二乘解

对​E_{(w,b)}=\sum_{i=1}^m\left(y_i-wx_i-b\right)^2进行最小二乘参数估计

什么是最小二乘参数估计？

分别对​w\text{ 和 }b求导

​\begin{aligned}&\begin{aligned}\frac{\partial E_{(w,b)}}{\partial w}\end{aligned}=2\left(w\sum_{i=1}^mx_i^2-\sum_{i=1}^m\left(y_i-b\right)x_i\right) \\&\begin{aligned}\frac{\partial E_{(w,b)}}{\partial b}\end{aligned} =2\left(mb-\sum_{i=1}^m\left(y_iwx_i\right)\right)\end{aligned}

令导数为 0,得到闭式(closed-form)解：

​w=\frac{\sum\limits_{i=1}^{m}y_i\left(x_i-\bar{x}\right)}{\sum\limits_{i=1}^{m}x_i^2-\frac{1}{m}\left(\sum\limits_{i=1}^{m}x_i\right)^2}\quad b=\frac{1}{m}\sum\limits_{i=1}^{m}\left(y_i-wx_i\right)

为什么求偏导视频讲解

3.3 多元线性回归

多元 Multi-variate

​f\left(\boldsymbol{x}_i\right)=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}_i+b\text{ 使得 }f\left(\boldsymbol{x}_i\right)\simeq y_i

​\boldsymbol{x}_i=(x_{i1};x_{i2};\ldots;x_{id})\quad\quad\quad y_i\in\mathbb{R}

注：在西瓜书中“，”表示行向量“；”表示列向量

​\text{把}w\text{和 }_b\text{吸收入向量形式 }\hat{\boldsymbol{w}}=(\boldsymbol{w};b)\text{数据集表示为}

​\mathbf{X}=\begin{pmatrix}x_{11}&x_{12}&\cdots&x_{1d}&1\\x_{21}&x_{22}&\cdots&x_{2d}&1\\\vdots&\vdots&\ddots&\vdots&\vdots\\x_{m1}&x_{m2}&\cdots&x_{md}&1\end{pmatrix}=\begin{pmatrix}\boldsymbol{x}_1^\mathrm{T}&1\\\boldsymbol{x}_2^\mathrm{T}&1\\\vdots&\vdots\\\boldsymbol{x}_m^\mathrm{T}&1\end{pmatrix}\quad\boldsymbol{y}=(y_1;y_2;\ldots;y_m)

同样采用最小二乘法求解，有：

令 ​E_{\hat{w}}=\left(\boldsymbol{y}-\mathbf{X}\hat{w}\right)^{\mathrm{T}}\left(\boldsymbol{y}-\mathbf{X}\hat{w}\right) ,对​\hat{w} 求导：

难点在于矩阵求导

​\text{若 }\mathbf{X}^\mathrm{T}\mathbf{X}\text{ 满秩或正定,则}\hat{\boldsymbol{w}}^*=\left(\mathbf{X}^\mathrm{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathrm{T}\boldsymbol{y}

​\text{若 }\mathrm{X}^\mathrm{T}\mathrm{X}\text{ 不满秩,则可解出多个}\hat{w}，此时需求助于归纳偏好，或引入正则化(regularization)

3.4 广义线性模型

很巧妙的思想

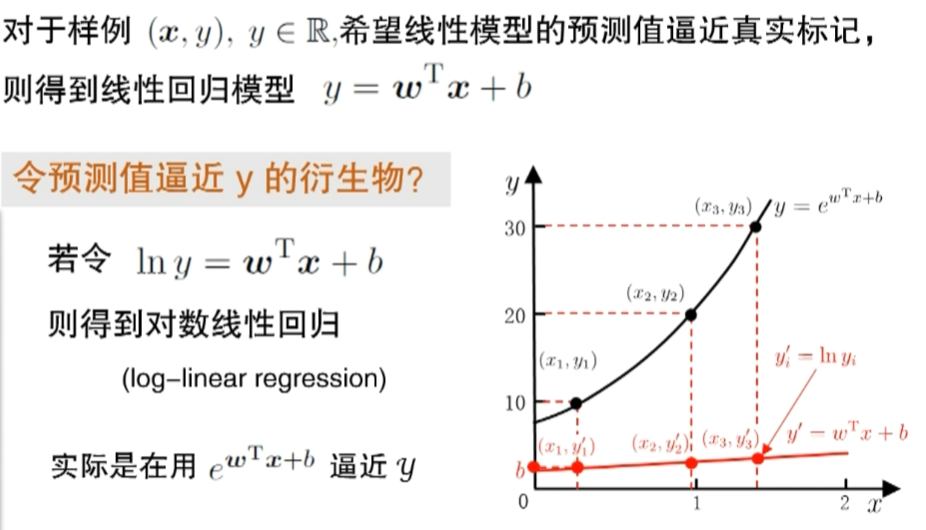
3.5 对率回归

二分类任务

​\text{线性回归模型产生的实值输出 }z=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b

​\text{期望输出 }y\in\{0,1\}，所以就要找z与y的联系函数

理想的“单位阶跃函数”(unit-step function)：

这个函数性质不好，需要找“替代函数”，要常用、单调可微、任意阶可导

因此找到了这样一个函数：

对数几率函数(logistic function)，简称对率函数

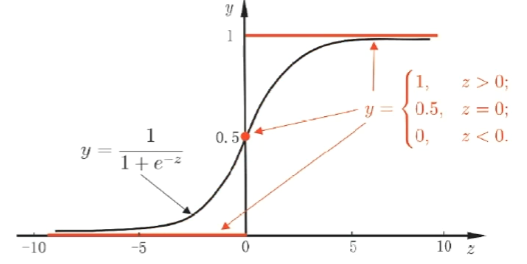
该函数的图像近似于第一开始的直线

以对率函数变为联系函数：

• ​y=\frac1{1+e^{-z}}\quad\text{变为}\quad y=\frac1{1+e^{-(\boldsymbol{w^\mathrm{T}x+b})}}

• 即​\ln\frac y{1-y}=w^\mathrm{T}x+b

  ​\frac{y}{1-y}，几率(odds)，反映了x作为正例的相对可能性

  对数几率(log odds,亦称尔logit)

  “对数几率回归”(logistic regression)，简称“对率回归”

  好处：

  • 无需事先假设数据分布
  • 可得到“类别”的近似概率预测
  • 可直接应用现有数值优化算法求取最优解

  注意：他是一个分类学习算法

3.6 对率回归求解

若将y看作类后验概率估计​p\left(y=1\mid x\right)，则​\ln\frac{y}{1-y}=\boldsymbol{w^\mathrm{T}}x+b\quad\text{可写为}\quad\ln\frac{p\left(y=1\mid\boldsymbol{x}\right)}{p\left(y=0\mid\boldsymbol{x}\right)}=\boldsymbol{w^\mathrm{T}}\boldsymbol{x}+b

于是，可使用**“极大似然法”**(maximumlikelihoodmethod)

第七章详细，概率论也学过

给定数据集​\{(\boldsymbol{x}_i,y_i)\}_{i=1}^m

最大化“对数似然”(log-likelihood)函数​\ell(\boldsymbol{w},b)=\sum_{i=1}^m\ln p(y_i\mid\boldsymbol{x}_i;\boldsymbol{w},b)

​\text{令 }\beta=(\boldsymbol{w};b),\hat{\boldsymbol{x}}=(\boldsymbol{x};1),\text{则 }w^\mathrm{T}\boldsymbol{x}+b\text{ 可简写为}\beta^\mathrm{T}\hat{\boldsymbol{x}}

​\text{再令 }p_1\left(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta}\right)=p\left(y=1\mid\hat{\boldsymbol{x}};\boldsymbol{\beta}\right)=\frac{e^{\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b}}{1+e^{\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b}}

​p_0\left(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta}\right)=p\left(y=0\mid\hat{\boldsymbol{x}};\boldsymbol{\beta}\right)=1-p_1\left(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta}\right)=\frac{1}{1+e^{\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b}}

​\text{则似然项可重写为}p\left(y_i\mid\boldsymbol{x}_i;\boldsymbol{w}_i,b\right)=y_ip_1\left(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta}\right)+(1-y_i)p_0\left(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta}\right)

​\text{于是,最大化似然函数 }\ell(w,b)=\sum_{i=1}^m\ln p(y_i\mid\boldsymbol{x}_i;\boldsymbol{w},b)

​\text{等价为最小化}\quad\ell\left(\boldsymbol{\beta}\right)=\sum_{i=1}^{m}\left(-y_i\boldsymbol{\beta}^\mathrm{T}\hat{\boldsymbol{x}}_i+\ln\left(1+e^{\boldsymbol{\beta}^\mathrm{T}\hat{\boldsymbol{x}}_i}\right)\right)

视频讲解-一个很巧妙的求通项的方法

高阶可导连续凸函数，可用经典的数值优化方法如梯度下降法/牛顿法[BoydandVandenberghe,2004]

3.7 线性判别分析

(Linear Discriminant Analysis)

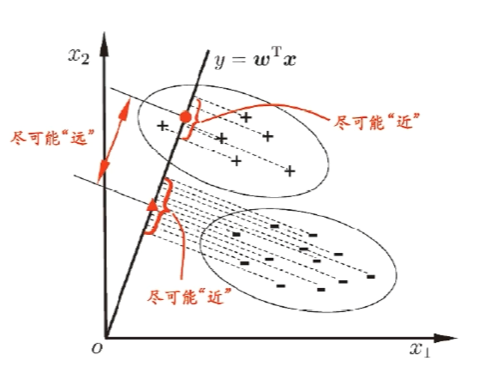
由于将样例投影到一条直线（低维空间），因此也被视为一种“监督降维”技术

降维第10章

给定数据集​\left\{\left(\boldsymbol{x}_i,y_i\right.\right\}_{i=1}^m

第 ​i 类示例的集合​X_i

第 ​i 类示例的协方差矩阵​\Sigma_i

两类样本的中心在直线上的投影：​w^\mathrm{T}\mu_0 和​w^\mathrm{T}\mu_1

两类样本的协方差：​w^\mathrm{T}\Sigma_0w 和 ​w^\mathrm{T}\Sigma_1w

同类样例的投影点尽可能接近 → ​w^\mathrm{T}\Sigma_0w+w^\mathrm{T}\Sigma_1w 尽可能小

异类样例的投影点尽可能远离 → ​\|w^\mathrm{T}_{\mu} ​\mu_{0}-w^{\mathrm{T}}\mu_{1}\|_{2}^{2} 尽可能大

于是，最大化​J=\frac{\left\|\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_1\right\|_2^2}{\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_1\boldsymbol{w}}=\frac{\boldsymbol{w}^\mathrm{T}\left(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\right)\left(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\right)^\mathrm{T}\boldsymbol{w}}{\boldsymbol{w}^\mathrm{T}\left(\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1\right)\boldsymbol{w}}

类内散度矩阵 (within-class scatter matrix)

类间散度矩阵 (between-class scatter matrix)

LDA的目标：最大化广义瑞利商 (generalized Rayleigh quotient)

整个起作用的是w的方向

令 ​w^\mathrm{T}\mathrm{S}_ww=1 最大化广义瑞利商等价形式为

​\text{运用拉格朗日乘子法,有 S}_b\boldsymbol{w}=\lambda\mathbf{S}_w\boldsymbol{w}

​\text{由 S}_b\text{定义,有 S}_b\boldsymbol{w}=\left(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\right)\left(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\right)^\mathrm{T}\boldsymbol{w}

​\text{注意到}\left(\mu_0-\mu_1\right)^{\mathrm{T}}w\text{标量,令其等于 }\lambda

3.8 类别不平衡

前面介绍的分类学习方法都有一个共同的基本假设，即不同类别的训练样例数目相当。如果不同类别的训练样例数目稍有差别，通常影响不大，但若差别很大，则会对学习过程造成困扰

例如有 998 个反例，但正例只有 个，那么学习方法只需返回一个永远将新样本预测为反例的学习器，就能达到 99.8% 的精度;然而这样的学习器往往没有价值，因为它不能预测出任何正例

类别不平衡(claimbalance)

我们要做处理的是丢掉的小类价值很高的情况

例如：信用卡欺诈检测，1000个中可能才会出现一个，但是这一个很重要

基本思路：

• ​\text{若 }\frac{y}{1-y}>1\text{ 则预测为正例}

  即y大于1/2

  我们现在认为正负同样重要

• ​\frac{m{+}}{m{-}}=\frac{1}{4}，则不以1/2为标准，变成以1/4为标准，大于1/4为正

  因此公式变为​\text{若 }\frac y{1-y}>\frac{m^+}{m^-}\text{则 预测为正例}

• 然而实际应用中，​\text{精确估计 }m^-/m^+\text{通常很困难}!，因为无法保证采样数据是真实数据的无偏真是采样

常见的类别不平衡学习方法：

• 过采样(oversampling)，例如：SMOTE

  让小类增加到与大类一样多

  最经典、最常用

  

• 欠采样（undersampling)，例如：EasyEnsemble

  把大类变小，变得跟小类一样多

  当然不可以随便丢，可能会给分类边界带来非常显著的变化

  EasyEnsemble：再做很多模型👇

  

  做了很多个模型之后，再用一些类似于投票一类的办法，让每个子模型均衡

• 阀值移动（threshold-moving)

  就是上面哪个概率变换

第五章 神经网络

5.1 神经网络模型

什么是神经网络？

• "神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应”

  [T.Kohonen,1988，NeuralNetworks创刊号]

• 神经网络是一个很大的学科领域，本课程仅讨论神经网络与机器学习的交集，即“神经网络学习”亦称“连接主义(connectionism)”学习

应用最广泛的神经元模型：

M-P神经元模型[McCulloch and Pitts, 1943]，即简单单元

类似于神经突触结构，一个神经细胞会接受来自其他细胞的信号，通过突触连接到达信号，传过来的实际是一个电位，当电位量到底一定阈值后，该神经细胞被激活，往外传出一个信号，可自行与图中简单单元一一对应

[接下来应该干什么工作呢，要求的其实还是w与b，给线性模型还是一样的](#3.1 线性回归)

每一个神经元本身，其实就是一个线性模型，有f以后便可以处理非线性的东西

f即为激活函数（响应函数、挤压函数）

12个激活函数详解

举例：[sigmoid函数](#3.5 对率回归)（常用）

• 可以理解为长得S型的，特性：​f^{\prime}(x)=f(x)(1-f(x))，恰恰是正负几率的乘积，非常优美
• 挤压：负无穷到正无穷的的输入挤压到了有限的y，因此叫挤压函数
• 是01损失的替代函数

多层前馈网络结构：（目前神经网络最常见的结构）

• 多层网络：包含隐层的网络

• 前馈网络：神经元之间不存在同层连接也不存在跨层连接

  意思就是不存在环

  

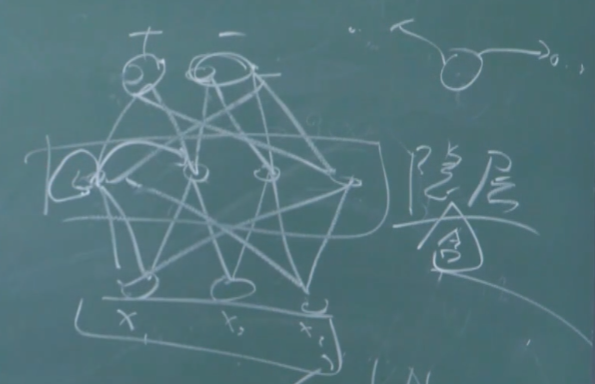
  上面这个的层数，如果按照功能神经元来说（带f的），是两层，为了避免歧义，所以说隐层，即单隐层

• 隐层和输出层神经元亦称“功能单元“(FunctionalUnit)

5.2 万有逼近能力

现在谈论5.1这样一个神经网络能力有多强，我们引入万有逼近能力

多层前馈网络有强大的表示能力（"万有逼近性”）

仅需一个包含足够多神经元的隐层，多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数[Horniketal.,1989]

为什么一个就可以，视频解释

延伸到，任何一个图灵可计算的问题，都可以找到一个一隐层神经网络做他的求解器

但是，如何设置隐层神经元数是未决问题（OpenProblem），实际常用“试错法”（其实就是猜，问题多就多设点）

万有逼近性不是神经网络的特性，只是它的一个前提，这个性质就是告诉我们，解已经在黑箱中了，我们要做的就是找到他

最简单的傅里叶变换都有万有逼近性（任何复杂的波形都可以通过一系列简单的正弦和余弦波的组合来表示）

5.3 BP算法推导

BP（BackPropagation:误差逆传播算法）

迄今最成功、最常用的神经网络算法，可用于多种任务

​\text{给定训练集}D=\{(x_1,y_1),(x_2,y_2),\ldots,(x_m,y_m)\},x_i\in\mathbb{R}^d,y_i\in\mathbb{R}^l

• 输入：d 维特征向量
• 输出：L个输出值
• 隐层：假定使用用9个隐层神经元

跳转Sigmoid 函数假定功能单元均使用Sigmoid 函数

将单个神经元拆分出：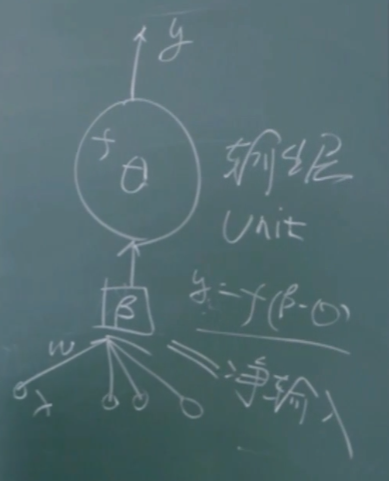

​\text{对于训练例 }(x_k,y_k)\text{,假定网络的实际输出为 }\hat{y}_k=(\hat{y}_1^k,\hat{y}_2^k,\ldots,\hat{y}_l^k)

​\text{那么，}\hat{y}_j^k=f(\beta_j-\theta_j)

​\text{则网络在 }(x_k,y_k)\text{上的均方误差为}:​E_k=\frac{1}{2}\sum_{j=1}^{l}(\hat{y}_j^k-y_j^k)^2

​\text{需通过学习确定的参数数目:}(d+l+1)q+l

BP 是一个迭代学习算法，在迭代的每一轮中采用广义感知机学习规则：

每轮需要改变的量是​\triangle v，有误差才需要改变，那么需要怎么来改他呢？

1.首先能想到的是，给这个变化求导，为了使其导数为零取极值点，对​\triangle v进行修改

2.通常神经网络中无法保证这个函数一定是凸的，但是我们求导之后，让函数往梯度的负方向走一定总归是好的

BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整：

​\text{以 }w_{hj}\text{ 为例}

​\text{对误差}E_k\text{,给定学习率 }\eta\text{,有}:​\Delta w_{hj}=-\eta\frac{\partial E_{k}}{\partial w_{hj}}

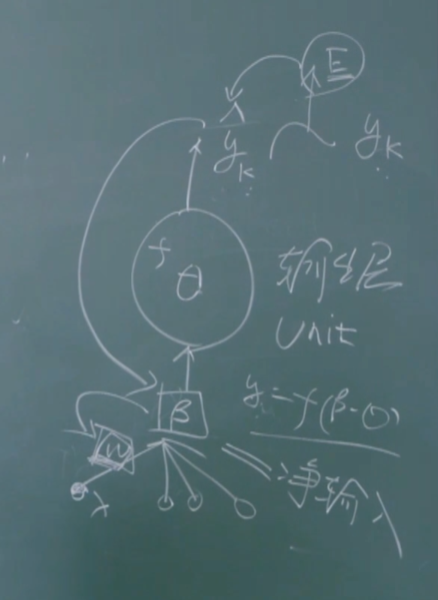
从上图可以得到，​w_{hj}\text{ 先影响到 }\beta_j\text{,再影响到 }\hat{y}_j^k\text{,然后才影响到}E_k\text{,有}:

继续化简：

注意到每个功能单元的函数性质，即可化简​f^{\prime}(\beta_j-\theta_j)为​\hat{y}_j^k(1-\hat{y}_j^k)

​\begin{aligned}\textit{令 }g_{j}& =-\frac{\partial E_{k}}{\partial\hat{y}_{j}^{k}}\cdot\frac{\partial\hat{y}_{j}^{k}}{\partial\beta_{j}} \\&=\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k)\end{aligned}

​\text{于是,}\Delta w_{hj}=-\eta\frac{\partial E_{k}}{\partial w_{hj}}=\eta g_{j}b_{h}

于是我们可以知道，整个​\Delta w_{hj}权重的调整就是由​g_{j}b_{h}决定的

同理可得：

​\text{学习率 }\eta\in(0,1)\text{ 不能太大、不能太小}

到这里，BP算法我们已经学会了！

整体再梳理一遍完整运行

最终能否收敛，取决于学习率​\text{n}的取值，动态学习率

对学习率的调节有可能出现震荡现象，跟嵌入式开发中调节电机的pid算法好像，可以类比理解

直接离目标值越远学习率越大

作微分，偏离目标的变化率越大，学习率减小

作积分，有扰动依旧可以保持

把数据集里每一个样本全部跟走一次，叫做完成了一轮训练

第六章 支持向量机

6.1 支持向量机基本型

[知识回顾](#3.1 线性回归)：

• 在样本空间中寻找一个超平面，将不同类别的样本分开
• 将训练样本分开的超平面可能有很多，哪一个更好呢？

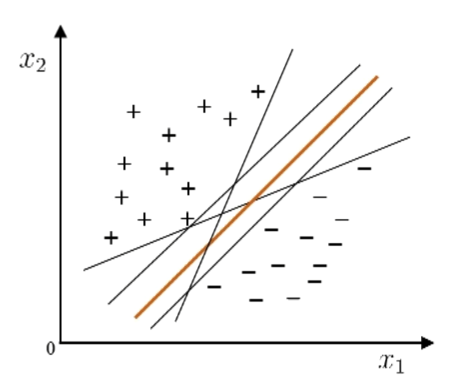
• 直觉上来说，正中间的最好，“正中间”的：鲁棒性最好，泛化能力最强

间隔（margin）与支持向量（support vector）：

• 超平面方程：​w^\top x+b=0

• 

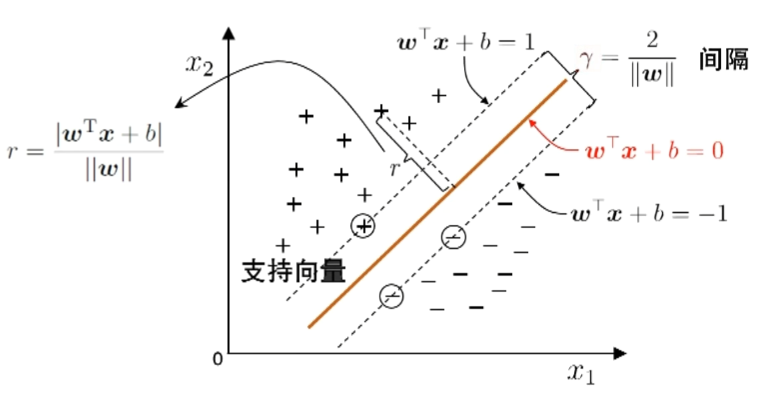
  一些小补充：

  • 什么是超平面（hyperplane）？

    超平面（hyperplane）是在更高维度中定义的一个概念，它是一个维数比其所嵌入的空间低一维的线性子空间。在二维空间中，超平面是一条直线；在三维空间中，它是一个平面。

    在更一般的情况下，假设我们有一个n维向量空间（n维空间），超平面是这个空间的一个n-1维子空间。换句话说，超平面将空间分成两个部分，其中一部分位于超平面的一侧，另一部分位于超平面的另一侧。

    超平面在机器学习和数据挖掘中经常被用来进行分类任务。例如，在支持向量机（Support Vector Machine）中，超平面用于分割不同类别的数据点。在这种情况下，超平面的选择旨在最大化两个类别之间的间隔，使得分类更加准确。

    总的来说，超平面是一个线性概念，但它的维度取决于所嵌入空间的维数。

  • ​\gamma=\frac{2}{\|\boldsymbol{w}\|}叫做超平面相对于整个数据集的间隔

    这个间隔决定了整个点到超平面距离的下界

  • 点到超平面的距离（间隔）如何计算？

    推导链接

    在距离计算中，出现两个绝对值符号通常是因为我们关心点到超平面的有符号距离。有符号距离表示点在超平面的一侧为正，另一侧为负。这对于分类问题是很重要的，因为我们想知道一个点是在超平面的哪一侧，以便进行分类预测。

    一个点离超平面的间隔越远，我们就说划分的越好，从几何上也是很好理解的

• 即我们现在的任务转化成了找最大间隔

最大间隔-​\text{寻找参数}w\text{ 和}b,\text{使得}\gamma\text{ 最大}：

• ​\begin{aligned}\arg\max&\frac{2}{\|\boldsymbol{w}\|}\\\mathrm{s.t.}&y_i(\boldsymbol{w}^\top\boldsymbol{x}_i+b)\geq1,i=1,2,\ldots,m.\end{aligned}

  ⬇️

  ​\begin{aligned}\arg\min_{\boldsymbol{w},b}&\frac12\|\boldsymbol{w}\|^2\\\mathrm{s.t.}&y_i(\boldsymbol{w}^\top\boldsymbol{x}_i+b)\geq1,i=1,2,\ldots,m.\end{aligned}

  凸二次规划问题，能用优化计算包求解，但可以有更高效的办法

  西瓜书讲解了更为简单的求解方式-拉格朗日乘子法

6.2 对偶问题与解的特性

什么是拉格朗日乘子法?

拉格朗日乘子法的基本思想是将带有约束条件的优化问题转化为一个不带约束条件的问题，通过引入拉格朗日乘子来考虑约束。

举例:

假设你是一个小型公司的经理，你的目标是最大化公司的利润。公司主要销售两种产品：产品 A 和产品 B。设 x 代表产品 A 的销售量，y 代表产品 B 的销售量。利润函数，即我们的目标函数 f(x, y)，可以表示为 f(x, y) = 40x + 30y，这里 40 和 30 分别是产品 A 和产品 B 单位销售的利润。

然而，由于生产能力的限制，你不能无限制地生产产品 A 和 B。设这个约束条件为 g(x, y) = 200 - 2x - 3y = 0，意味着产品 A 和 B 的生产量之和不能超过 200 个单位。

现在，我们需要构建一个拉格朗日函数 L(x, y, λ) 来解决这个优化问题。函数为 L(x, y, λ) = 40x + 30y - λ * (200 - 2x - 3y)。

接下来的步骤是：

求偏导数：

• 对 x 求偏导：Lx = d/dx(40x + 30y - λ * (200 - 2x - 3y)) = 40 + 2λ。
• 对 y 求偏导：Ly = d/dy(40x + 30y - λ * (200 - 2x - 3y)) = 30 + 3λ。
• 对 λ 求偏导：Lλ = d/dλ(40x + 30y - λ * (200 - 2x - 3y)) = -200 + 2x + 3y。

设偏导数为零求解：

• 设 Lx = 0，得到 40 + 2λ = 0。
• 设 Ly = 0，得到 30 + 3λ = 0。
• 设 Lλ = 0，得到 -200 + 2x + 3y = 0。

解方程组：

• 从 Lx = 0 和 Ly = 0，我们可以解出 λ。
• 然后代入 Lλ = 0 的方程中，解出 x 和 y。

假设通过计算，我们得到 x = 50，y = 40，λ = -20。这意味着在生产能力的约束下，生产 50 个产品 A 和 40 个产品 B 可以使得公司的利润最大化。

使用拉格朗日乘子法求最大间隔:

• 第一步：引入拉格朗日乘子​\alpha_i\geq0得到拉格朗日函数

  L(\boldsymbol{w},b,\boldsymbol{\alpha})=\frac{1}{2}\:\|\boldsymbol{w}\|^{2}+\sum_{i=1}^{m}\alpha_{i}\:\big(1-y_{i}(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}_{i}+b)\big)

  在这个推导中，​y_i 是训练样本 ​\boldsymbol{x}_i 的标签（类别），取值为+1或-1。在支持向量机的问题中，我们通常考虑的是一个二分类问题，标签 ​y_i 表示样本 ​\boldsymbol{x}_i 的类别，+1 表示正类别，-1 表示负类别。

• 第二步：令​L(\boldsymbol{w},b,\boldsymbol{\alpha}) 对​w 和​b的偏导为零可得

  \boldsymbol{w}=\sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i\:,\quad0=\sum_{i=1}^m\alpha_iy_i

• 但实际上，我们求得的这个解,对于原来的问题是一个对偶问题

  什么是对偶问题

  对偶问题是数学和优化理论中与原始问题相对应的一个问题。对于给定的原始问题，通过构造拉格朗日函数并利用拉格朗日乘子法，可以得到一个对偶问题。这两个问题通常是紧密联系的，解决其中一个问题的信息可以用来解决另一个问题。

  考虑一个带有约束条件的优化问题，一般形式如下：
  最小化 ​f(x)
  约束条件 ​g_i(x)\leq0,\quad i=1,2,\ldots,m

  对应的拉格朗日函数为：
  ​L(x,\lambda)=f(x)+\sum_{i=1}^m\lambda_ig_i(x)
  其中，​\lambda_i 是拉格朗日乘子。

  对偶问题的目标是通过最大化拉格朗日函数关于拉格朗日乘子入的下确
  界，即：
  ​\theta(\lambda)=\inf_xL(x,\lambda)
  对于每个​\lambda_i\geq0。

  对偶问题的一般形式如下：
  最大化 ​\theta(\lambda)
  约束条件 ​\lambda_i\geq0,\quad i=1,2,\ldots,m

• 第三步：回代可得

  \begin{aligned}\max_{\alpha}&\quad\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^\mathrm{T}\boldsymbol{x}_j\\\text{s.t.}&\quad\sum_{i=1}^m\alpha_iy_i=0,\alpha_i\geqslant0,\quad i=1,2,\ldots,m\end{aligned}

• 最终模型:​f(\boldsymbol{x})=\boldsymbol{w}^\top\boldsymbol{x}+b=\boxed{\sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i^\top\boldsymbol{x}}+b

  ​\begin{aligned}&\text{KKT条件:}\\\\&\begin{cases}&\alpha_i\geq0;\\\\&1-y_if(\boldsymbol{x}_i)\leq0;\\\\&\alpha_i\left(1-y_if(\boldsymbol{x}_i)\right)=0.\end{cases}\end{aligned}​\Longrightarrow ​\begin{aligned}&\text{必有 }\alpha_i=0\text{或}\\&y_if(\boldsymbol{x}_i)=1\end{aligned}

• 我们分析这个结果：

  ​\alpha_{i}=0表示已其为系数的点在函数中没有出现

  ​y_if(\boldsymbol{x}_i)=1表示恰好在超平面的间隔上

• 解的稀疏性训练完成后，最终模型仅与支持向量有关

  支持向量机(SupportVectorMachine，SVM）因此而得名

6.3 求解方法

在第二节求解的时候，我们直接给出了解探究其特性，这一节我们回到公式，探究具体求解的方法

对于回代得到的式子，有好多现成的包可以进行计算，本节我们学习更快速的方法

思路：我们每次只考虑i与j，那么其余m-2个就都可以看成常数

求解方法-SMO（最经典最著名）：

基本思路：不断执行如下两个步骤直至收敛

• ​\text{第一步:选取一对需更新的变量}\alpha_i\text{ 和 }\alpha_j
• ​\text{第二步:固定 }\alpha_i\text{和 }\alpha_j\text{以外的参数,求解对偶问题更新 }\alpha_i\text{ 和 }\alpha_j

仅考虑​\alpha_i和​\alpha_j时，对偶问题的约束 0​=\sum\alpha_iy_i 变为

用 ​\alpha_i 表示 ​\alpha_j,代入对偶问题

违反KKT条件越多的解，我们越拿他来训练函数，就这样一直找，知道最后收敛

​\text{对任意支持向量}(x_s,y_s)\text{有 }y_sf(x_s)=1\text{ 由此可解出 }b

从最终式看，只需解出一个解，就可以得出b，但是为提高鲁棒性，通常使用所有支持向量求解的平均值

6.4 特征空间映射

若不存在一个能正确划分两类样本的超平面，怎么办?

将样本从原始空间映射到一个更高维的特征空间，使样本在这个特征空间内线性可分

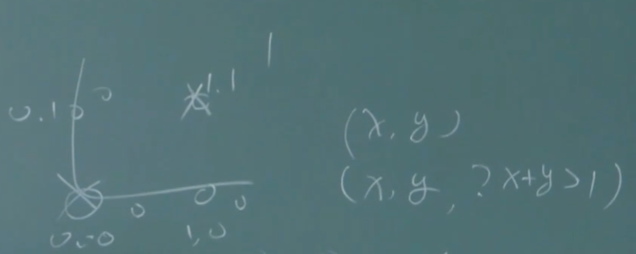
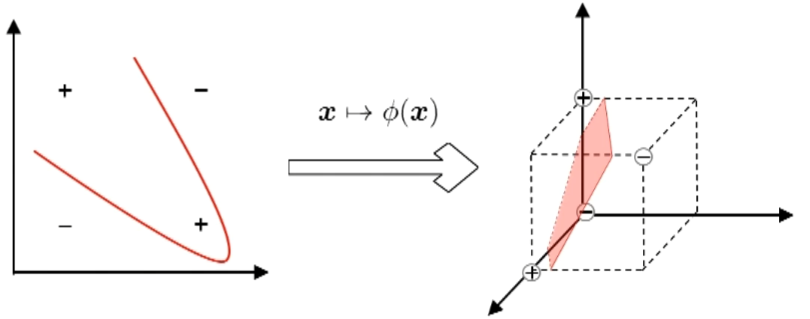
如果原始空间是有限维(属性数有限)，那么一定存在一个高维特征空间使样本线性可分

这个高维可能是无限维

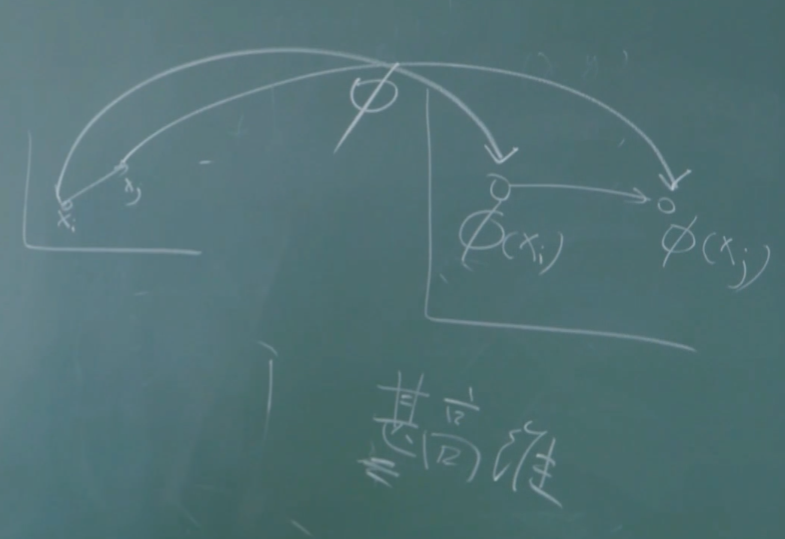
设样本​x 映射后的向量为​\phi(x),划分超平面为​f(x)=\boldsymbol{w}^\top\phi(\boldsymbol{x})+b

​\textbf{原始问题}\quad\boxed{\begin{array}{rl}\min_{w,b}&\frac12\|\boldsymbol{w}\|^2\\\mathrm{s.t.}&y_i(\boldsymbol{w}^\top\phi(\boldsymbol{x}_i)+b)\geq1,i=1,2,\ldots,m.\end{array}}

​\textbf{对偶问题}\quad\boxed{\begin{aligned}\max_\alpha & \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \phi(x_i)^\mathrm{T} \phi(x_j) \\\mathrm{s.t.} & \sum_{i=1}^m \alpha_i y_i = 0, \quad \alpha_i \geqslant 0, \quad i=1,2,\ldots,m\end{aligned}}

难点在于两个高维向量的内积计算十分困难

​\text{预测}\quad f(\boldsymbol{x})=\boldsymbol{w}^\mathrm{T}\phi(\boldsymbol{x})+b=\sum_{i=1}^m\alpha_iy_i\underline{\phi(\boldsymbol{x}_i)^\mathrm{T}\phi(\boldsymbol{x})}+b

化简启发：我们可以发现高维向量只以内积形式出现

6.5 核函数

解决6.4计算高维向量内积的问题

基本思路：设计核函数

绕过显式考虑特征映射、以及计算高维内积的困难

Mercer定理：若一个对称函数所对应的核矩阵半正定，则它就能作为核函数来使用

• 矩阵半正定：

  一个矩阵被称为半正定（positive semi-definite）是指对于任何非零的实向量 x，都有 x^T A x ≥ 0，其中 A 是这个矩阵。

  换句话说，对于一个半正定矩阵，任何非零向量经过矩阵的乘法后，其内积（乘积的转置再乘以原向量）都是非负的。这类矩阵在数学和工程中有广泛的应用，尤其在线性代数、优化问题、概率论和统计学等领域。

  如果在定义中加上 "正定" 的条件，那么这意味着对于任何非零的实向量 x，都有 x^T A x > 0，其中不等式中的大于号表示严格大于。这样的矩阵被称为正定矩阵。半正定矩阵则包括了非负的情况，即可以取到零。

• 对函数重新认识：

  函数其实就是对空间的一种变换

  

  每个点之间的相互关系会发生一定的扭曲

  当两点之间的距离确定下来以后，我们就说它在这个甚高维中的位置确定了

  

• 核矩阵：

  包含了所有样本的一个距离矩阵，恰恰表达了某一个空间，那么他就可以当成一个核函数来使用

任何一个核函数，都隐式地定义了一个RKHS（ReproducingKernel HilbertSpace,再生核希尔伯特空间)

核矩阵、核函数、RKHS、​\phi 的关系解读

“核函数选择”成为决定支持向量机性能的关键！

6.6 如何使用SVM

SVM，或支持向量机（Support Vector Machine），是一种在监督学习中用于分类和回归的机器学习算法。它的主要目标是找到一个超平面，该超平面能够在高维空间中有效地将不同类别的数据点分开。

以回归学习为例：

基本思路：​允许模型输出与实际输出间存在2\epsilon 的差别

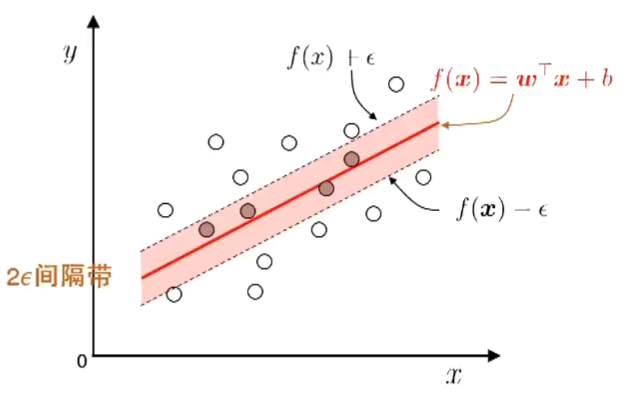
​\epsilon -不敏感（insensitive）损失函数：

落入​2\epsilon 间隔带的样本不计算损失

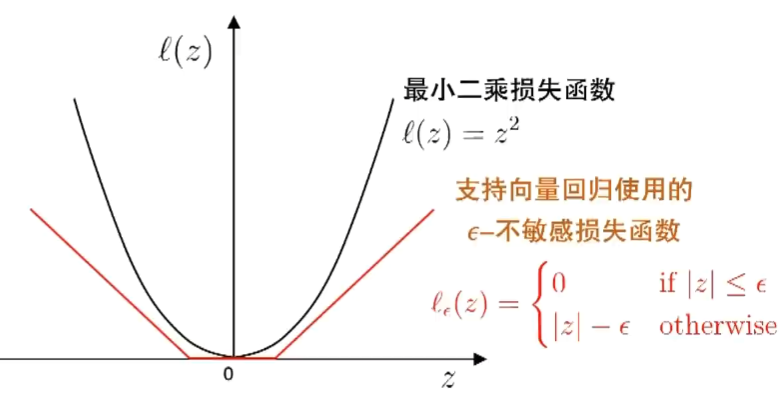
支持向量回归（SVR）：

原始问题：​\boxed{\begin{aligned}\min_{\boldsymbol{w},\boldsymbol{b},\boldsymbol{\xi}_i,\hat{\boldsymbol{\xi}_i}}\frac12\|\boldsymbol{w}\|^2+C\sum_{i=1}^m(\xi_i+\hat{\boldsymbol{\xi}_i})\\\text{s.t. }f(\boldsymbol{x}_i)-y_i\leqslant\epsilon+\xi_i,\\y_i-f(\boldsymbol{x}_i)\leqslant\epsilon+\hat{\boldsymbol{\xi}_i},\\\zeta_i\geqslant0,\hat{\boldsymbol{\zeta}_i}\geqslant0,i=1,2,\ldots,m\end{aligned}}

对偶问题：​\boxed{\begin{aligned}\max_{\alpha,\alpha}&\sum_{i=1}^my_i(\hat{\alpha}_i-\alpha_i)-\epsilon(\hat{\alpha}_i+\alpha_i)-\frac12\sum_{i=1}^m\sum_{j=1}^m(\hat{\alpha}_i-\alpha_i)(\hat{\alpha}_j-\alpha_j)x_i^\mathrm{T}x_j\\\text{s.t.}&\sum_{i=1}^m(\hat{\alpha}_i-\alpha_i)=0,0\leqslant\alpha_i,\hat{\alpha}_i\leqslant C\end{aligned}}

预测：​f(\boldsymbol{x})=\sum_{i=1}^m(\hat{\alpha}_i-\alpha_i)\boldsymbol{x}_i^\mathrm{T}\boldsymbol{x}+b

显示应用中，如何使用SVM？

• 入门级—— 实现并使用各种版本SVM
• 专业级——尝试、组合核函数
• 专家级——根据问题而设计目标函数、
  替代损失、进而.........

第十二章 计算学习理论

12.1 基础知识

这一章要解决什么问题？

顾名思义，计算学习理论(computational learning theory)研究的是关于通 过"计算"来进行"学习"的理论，即关于机器学习的理论基础，其目的是分 析学习任务的困难本质，为学习算法提供理论保证，并根据分析结果指导算法设计

例如，如果我们想知道一个模型正确率的上限是多少，如果没有学过第十二章，只能是通过不断地更换参数，随机性的探索这个模型到底合不合适，正确率可能能达到什么样的高度，但是通过这一章的学习，我们就可以在拿到这个模型的时候，通过理论计算得到它的上限，来迅速判断是否选择、使用这个模型

但实际上，这一章其实还停留在理论上，不会对实际应用中起到太大的帮助

背景交代：

给定样例集​D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),\ldots,(\boldsymbol{x}_m,y_m)\},\boldsymbol{x}_i\in\mathcal{X}， 本章主要讨论二分类这一个简单但是通用的问题

若无特别说明，​y_i\in\mathcal{Y}=\{-1,+1\}.假设​\chi 中的所有样本服从一个隐含未知的分布​D,D 中所有样本都是独立地从这个分布上采样而得，即独立同分布 (independent and identically distributed, 简称 ​i.i.d.) 样本

独立同分布是在理想化条件下的

令​h 为从 ​x 到 ​\gamma 的一个映射，其泛化误差为

​h 在 ​D 上的经验误差为

泛化误差就是测试集上的误差，所以x是从花D里面采样

经验误差就是在训练集上的误差，x已经拿到了，所以个数已知为m

由于​D 是 ​\mathcal{D} 的独立同分布采样，因此 ​h 的经验误差的期望等于其泛化误差.在上下文明确时，我们将​E(h;\mathcal{D}) 和​\widehat{E}(h;D) 分别简记为​E(h) 和​\widehat{E}(h).令​\epsilon 为 ​E(h) 的上限，即 ​E( h) \leqslant \epsilon; 我们通常用​\epsilon 表示预先设定的学得模型所应满足的误差要求，亦称“误差参数”

这里的​\epsilon 即为我们追求的“正确率”上限

本章后面部分将研究经验误差与泛化误差之间的逼近程度. 若 ​h 在数据集​D 上的经验误差为 0,则称 ​h 与 ​D 一致（D是训练集，可以训练到误差为0），否则称其与 ​D 不一致. 对任意两个映射​h_1,h_2\in\mathcal{X}\to\mathcal{Y},可通过其“不合”(disagreement)来度量它们之间的差别：

d有距离、差距的意思，通过他们两个结果不同的概率描述两个模型之间的差别

这章会常用到的几个不等式：

• Jensen 不等式：对任意凸函数 ​f(x), 有

  f(\mathbb{E}(x))\leqslant\mathbb{E}(f(x))\mathrm{~.}

  有个坑，凹凸函数的定义实际上是比较混乱的

  这里的凸函数图像是U型的，可以画图简单理解

• Hoeffding 不等式（第八章用过） [Hoeffding, 1963]: 若 ​x_1,x_2,\ldots,x_m 为 ​m 个独立随机变量，且满足 ​0\leqslant x_i\leqslant1, 则对任意 ​\epsilon>0, 有

  P\left(\frac1m\sum_{i=1}^mx_i-\frac1m\sum_{i=1}^m\mathbb{E}(x_i)\geqslant\epsilon\right)\leqslant\exp(-2m\epsilon^2)\:.
  P\left(\left|\frac1m\sum_{i=1}^mx_i-\frac1m\sum_{i=1}^m\mathbb{E}(x_i)\right|\geqslant\epsilon\right)\leqslant2\exp(-2m\epsilon^2)\:.

  可以从波动概率层面理解，前面的波动肯定大于后面，其实我认为是Jensen 不等式的升级版

  使用大数定理、中心极限定理证明

• McDiarmid 不等式[McDiarmid, 1989]: 若 ​x_1,x_2,\ldots,x_m 为 ​m 个独立随机变量，且对任意 ​1\leqslant i\leqslant m, 函数​f 满足

  \sup_{x_1,...,x_m,x_i^{\prime}}|f(x_1,\ldots,x_m)-f(x_1,\ldots,x_{i-1},x_i^{\prime},x_{i+1},\ldots,x_m)|\leqslant c_i\mathrm{~,}

  sup表示上界

  m个数据点我换掉一个，假设f是其的一个损失函数，现在就探讨其某一次试验与数学期望的关系有多大，对结果的影响有多大

  现在只是对其的一个笼统解释，真正理解需要结合实际来说

  则对任意 ​\epsilon>0, 有

  P\left(f\left(x_1,\ldots,x_m\right)-\mathbb{E}\left(f\left(x_1,\ldots,x_m\right)\right)\geqslant\epsilon\right)\leqslant\exp\left(\frac{-2\epsilon^2}{\sum_ic_i^2}\right).
  P\left(\left|f\left(x_1,\ldots,x_m\right)-\mathbb{E}\left(f\left(x_1,\ldots,x_m\right)\right)\right|\geqslant\epsilon\right)\leqslant2\exp\left(\frac{-2\epsilon^2}{\sum_ic_i^2}\right)\:.

12.2 PAC学习

Probably Approximately Correct，就是前面（1.4）提到的“概率近似正确”

概率近似正确：最后的结果好不好，是一个概率的事情，我们的模型通过不断的参数选取，有一定的概率达到某一个精确度，即“概率近似正确”

还是在12.1交代的二分类问题下：

令​c 表示“概念”(concept), 这是从样本空间​\chi 到标记空间 ​\gamma 的映射，它决定示例 ​x 的真实标记 ​y, 若对任何样例 ​(\boldsymbol{x},y) 有 ​c(\boldsymbol{x})=y 成立，则称 ​c 为目标概念；所有我们希望学得的目标概念所构成的集合称为“概念类”(concept class), 用符号​\mathcal{C}表示

以猫和狗的分类器为例，他真的能认识猫和狗吗？分类器用来识别猫和狗所建立的概念与“猫”“狗”的概念一样吗？

对于我们这个二分类问题来说，我们把这个分类器得到的“猫”的概念成为上述概念c，我们真正希望学到的“猫”的概念为上述概念类​\mathcal{C}

给定学习算法​{\mathfrak{L}},它所考虑的所有可能概念的集合称为“假设空间”(hypothesis space), 用符号 ​\mathcal{H}表示. 由于学习算法事先并不知道概念类的真实存在，因此和​\mathcal{H}与​\mathcal{C}通常是不同的，学习算法会把自认为可能的目标概念集中起来构成 ​\mathcal{H},​\text{对 }h\in\mathcal{H},由于并不能确定它是否真是目标概念，因此称为“假设”(hypothesis).显然，假设​h 也是从样本空间​\chi 到标记空间 ​\gamma 的映射

其实对上述两段进行理解，花写的字母类似于面向对象编程中的类，小写的字母是其的实例

​\mathcal{H}是我们的算法竭尽所能能囊括进来了概念的集合

​\mathcal{C}是我们想让他有的概念的集合

就算我们得到的正确率为百分之百了，全部满足训练数据了，我们也称之为假设hypothesis

若目标概念​c\in\mathcal{H},则​\mathcal{H} 中存在假设能将所有示例按与真实标记一致的方式完全分开，我们称该问题对学习算法 ​{\mathfrak{L}}是“可分的”(separable), 亦称“一致的”(consistent);若​c\notin\mathcal{H},则​\mathcal{H}中不存在任何假设能将所有示例完全正确分开；称该问题对学习算法​{\mathfrak{L}}是“不可分的”(non-separable), 亦称“不一致的”(non-consistent)

​c\in\mathcal{H}，就说明我这个算法有这个能力，能够部分的解决问题

​c\notin\mathcal{H}，也不能说这个算法没有用，可能四分类中能分出两个

给定训练集 ​D, 我们希望基于学习算法​{\mathfrak{L}}学得的模型所对应的假设 ​h 尽可能接近目标概念 ​c

为什么不是希望精确地学到目标概念 ​c 呢？

这是由于机器学习过程受到很多因素的制约，例如我们获得的训练集 ​D 往往仅包含有限数量的样例，因此，通常会存在一些在​D上“等效”的假设，学习算法对它们无法区别；再如，从分布 ​\mathcal{D} 采样得到 ​D 的过程有一定偶然性，可以想象，即便对同样大小的不同训练集，学得结果也可能有所不同. 因此，我们是希望以比较大的把握学得比较好的模型，也就是说，以较大的概率学得误差满足预设上限的模型；这就是“概率”“近似正确”的含义

形式化的说，令​{\boldsymbol{\delta}}表示置信度，可定义：

PAC 辨识 (PAC Identify): 对 ​0<\epsilon,\delta<1, 所有 ​c\in\mathcal{C} 和分布​\mathcal{D},若存在学习算法 ​{\mathfrak{L}}, 其输出假设 ​h\in\mathcal{H} 满足

则称学习算法 ​{\mathfrak{L}} 能从假设空间 ​\mathcal{H} 中 PAC 辨识概念类 ​\mathcal{C}

错误率能够以一定概率小于一个数

✨PAC 可学习 (PAC Learnable): 令 ​m 表示从分布 ​\mathcal{D} 中独立同分布采样得到的样例数目，​0<\epsilon,\delta<1, 对所有分布 ​\mathcal{D} , 若存在学习算法 ​{\mathfrak{L}} 和多项式函数 poly​(\cdot,\cdot,\cdot,\cdot), 使得对于任何 ​m\geqslant poly​( 1/\epsilon, 1/\delta, size​( \boldsymbol{x}) , size​( c) ) , ​{\mathfrak{L}} 能从假设空间​\mathcal{H}中 PAC 辨识概念类​\mathcal{C}, 则称概念类​\mathcal{C} 对假设空间 ​\mathcal{H} 而言是 PAC 可学习的，有时也简称概念类​\mathcal{C} 是 PAC 可学习的

样例数目 ​m 与误差 ​\epsilon、 置信度​\delta 、数据本身的复杂度 size​(x)、目标概念的复杂度 size(c) 都有关.

很关键的一个东西，我们通常觉得样本点越多越好，可是这是有成本的，PAC可学习就定义了一件事情，我们这个数据到底要到达一个什么样的程度才行

算法的样本复杂度

对计算机算法来说，必然要考虑时间复杂度，于是:

PAC 学习算法 (PAC Learning Algorithm): 若学习算法 ​{\mathfrak{L}} 使概念类​c 为 PAC 可学习的，且​{\mathfrak{L}} 的运行时间也是多项式函数 poly​(1/\epsilon,1/\delta, size​( \boldsymbol{x}) , size​( c) ) , 则称概念类​C 是高效 PAC 可学习 (efficiently PAC learnable) 的，称 ​{\mathfrak{L}}为概念类 ​\mathcal{C} 的 PAC 学习算法

其实很好理解，我们的运算时间跟误差 ​\epsilon、 置信度​\delta 、数据本身的复杂度 size​(x)、目标概念的复杂度 size(c) 呈一个多项式关系，而不是要求提升一点点时间就成倍增长，就说明 ​{\mathfrak{L}}还可以

上面这几个概念其实都是一些约定

样本复杂度 (Sample Complexity): 满足 PAC 学习算法 ​{\mathfrak{L}} 所需的 ​m\geqslant poly​( 1/\epsilon, 1/\delta, size​( \boldsymbol{x}) , size​( c) ) 中最小的 ​m, 称为学习算法 ​{\mathfrak{L}} 的样本复杂度

综上所述：

PAC 学习给出了一个抽象地刻画机器学习能力的框架，基于这个框架能对很多重要问题进行理论探讨，例如研究某任务在什么样的条件下可学得 较好的模型?某算法在什么样的条件下可进行有效的学习?需多少训练样例才 能获得较好的模型?

现在进行一个讨论：

其实跟过拟合欠拟合的概念类似

12.3 有限假设空间

12.2给出的大部分都是定义，12.3进行的是一波更细致的讨论，一些参数要满足什么什么条件才行

我要多少的数据，才可以达到什么样的正确率的讨论

12.3.1 可分情形

人话，能把训练集上的照片分个八九不离十，你也别管它现在有没有过拟合欠拟合

可分情形意味着目标概念 ​c 属于假设空间 ​\mathcal{H},即 ​c\in\mathcal{H}. 给定包含 ​m 个样例的训练集D , 如何找出满足误差参数的假设呢？

出现错误的假设就剔除，知道仅剩下一个假设为止

但由于训练数据是有限的，所以可能不止一个假设，会出现很多等效假设

这里我们直接给出这一节唯一有用的公式：

12.3.2 不可分情形

对较为困难的学习问题，目标概念 ​c 往往不存在于假设空间 ​\mathcal{H} 中. 假定对于任何​h\in\mathcal{H},\widehat{E}(h)\neq0,也就是说，​\mathcal{H}中的任意一个假设都会在训练集上出现或多或少的错误.由 Hoeffding 不等式易知：

引理 12.1 若训练集 ​D 包含 ​m 个从分布 ​\mathcal{D} 上独立同分布采样而得的样例，​0<\epsilon<1, 则对任意 ​h\in\mathcal{H},有

推论 12.1 若训练集 ​D 包含 ​m 个从分布 ​\mathcal{D} 上独立同分布采样而得的样例​,0<\epsilon<1,则对任意​h\in\mathcal{H},下面的式子以至少 ​1-\delta 的概率成立：

推论 12.1表明，样例数目 ​m 较大时，​h 的经验误差是其泛化误差很好的近似.对于有限假设空间 ​\mathcal{H},我们有

定理 12.1 若 ​\mathcal{H} 为有限假设空间，​0<\delta<1, 则对任意 ​h\in\mathcal{H},有

E(h)是错误率，​\widehat{E}(h)是当前这个模型整个错误率的数学期望

PAC 辨识 (PAC Identify)公式的更具体化

不可知PAC可学习

12.4 VC维

在前面三节中，还是有一个不能算的量 ​\mathcal{H}，这节中我们就把他给具体化，希望可以度量假设空间的复杂度

介绍VC维之前，我们先引入几个简单的概念：

给定假设空间​\mathcal{H} 和示例集 ​D=\{\boldsymbol{x}_1,\boldsymbol{x}_2,\ldots,\boldsymbol{x}_m\},\mathcal{H} 中每个假设 ​h 都能对​D 中示例赋予标记，标记结果可表示为

随着m的增大，​\mathcal{H}中所有假设对D 中的示例所能赋予标记的可能结果数也会增大

譬如h1是通过西瓜外皮颜色来判断是好瓜还是坏瓜，h2通过西瓜大小来判断好瓜还是坏瓜

增长函数(growth function)：

对所有 ​m\in\mathbb{N},假设空间 ​\mathcal{H} 的增长函数 ​\Pi_{\mathcal{H}}(m) 为

增长函数 ​\Pi_{\mathcal{H}}(m) 表示假设空间 H 对 ​m 个示例所能赋予标记的最大可能结果数.显然，​\mathcal{H}对示例所能赋予标记的可能结果数越大，​\mathcal{H}的表示能力越强， 对学习任务的适应能力也越强. 因此，增长函数描述了假设空间 ​\mathcal{H} 的表示能力， 由此反映出假设空间的复杂度. 我们可利用增长函数来估计经验误差与泛化误差之间的关系：

• 对假设空间 ​\mathcal{H},m\in\mathbb{N},0<\epsilon<1 和任意 ​h\in\mathcal{H} 有

  P(|E(h)-\widehat{E}(h)|>\epsilon)\leqslant4\Pi_{\mathcal{H}}(2m)\exp{(-\frac{m\epsilon^2}8)}

  错误率与错误率的期望的差大于某个数值的概率，与12.3.2中的公式类似

  证明是一整篇论文，略

• ✨假设空间​\mathcal{H}中不同的假设对于​D 中示例赋予标记的结果可能相同，也可能不同；尽管 ​\mathcal{H} 可能包含无穷多个假设，但其对 ​D 中示例赋予标记的可能结果数是有限的：对 ​m 个示例，最多有 ​2^m 个可能结果. 对二分类问题来说，​\mathcal{H} 中的假设对​D 中示例赋予标记的每种可能结果称为对​D 的一种“对分”。若假设空间 ​\mathcal{H} 能实现示例集 ​D 上的所有对分，即 ​\Pi_{\mathcal{H}}(m)=2^m, 则称示例集 ​D 能被假设空间​\mathcal{H}“打散”

  对 ​m 个示例，最多有 ​2^m ,即01串的个数，显而易见

  对分：是好瓜是坏瓜，每一种可能性是一种对分

现在，我们可以正式定义VC维了：

假设空间​\mathcal{H}的 VC 维是能被​\mathcal{H} 打散的最大示例集的大小，即

"空间​\mathcal{H}的 VC 维"这个描述表明了VC维也是用来描述这个模型的能力的

VC​( \mathcal{H} ) = d 表明存在大小为 ​d 的示例集能被假设空间 ​\mathcal{H} 打散.注意：这并不意味着所有大小为​d 的示例集都能被假设空间 ​\mathcal{H} 打散. VC 维的定义与数据分布​\mathcal{D} 无关！因此，在数据分布未知时仍能计算出假设空间​\mathcal{H}的VC 维

通常这样来计算​\mathcal{H}的 VC 维：若存在大小为 ​d 的示例集能被 ​\mathcal{H} 打散，但不存在任何大小为 ​d+1 的示例集能被 ​\mathcal{H} 打散，则 ​\mathcal{H} 的 VC 维是 ​d.

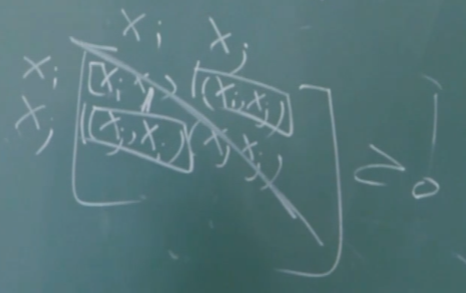
还是没有理解VC维？没关系！我们通过两个书上的例子秒懂：

根据这两个生动的例子，我们可以得到增长函数与VC维的关系：

严谨的证明需要数学归纳法，这里我们直接用想的

推论：若假设空间 ​\mathcal{H} 的 VC 维为 ​d,则对任意整数 ​m\geqslant d 有

​\begin{aligned}\Pi_{\mathcal{H}}(m)& \leqslant\sum_{i=0}^d\binom mi \\&\leqslant\sum_{i=0}^d\binom mi\left(\frac md\right)^{d-i} \\&=\left(\frac md\right)^d\sum_{i=0}^d\binom mi\left(\frac dm\right)^i \\&\leqslant\left(\frac md\right)^d\sum_{i=0}^m\binom mi(\frac dm)^i \\&=\left(\frac md\right)^d\left(1+\frac dm\right)^m \\&\leqslant\left(\frac{e\cdot m}d\right)^d\end{aligned}

最终式：

若假设空间 ​\mathcal{H} 的 VC 维为 ​d, 则对任意​m> d, 0< \delta< 1 和​h\in\mathcal{H}有