填空题

  1. 遍历图的基本方法有深度优先搜索和广度优先搜索。
  2. 深度优先搜索适于用使用递归方法实现，广度优先搜索适于使用队列实现。
  3. 已知图有 n 个顶点和 e 条边，若图为有向图，采用邻接表存储，那么边结点有e个；若图为无向图，采用逆邻接表存储，边结点有2e个，用邻接多重链表存储，边结点有2e个。
  4. n 个顶点的连通图至少有n-1条边，而 n 个顶点的强连通图至少有n条弧。
  5. 从图中任意顶点出发，一次广度或深度优先遍历就能访问图中所有顶点（F）（判断： 说法正确写 T，错误写 F）

算法题

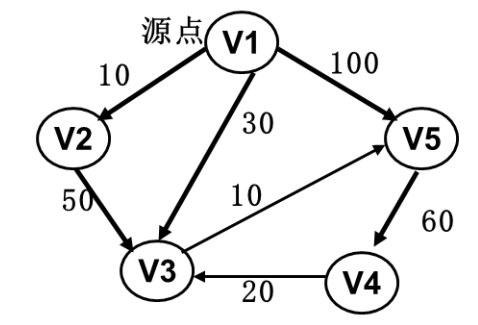
image-20231224190120689

  1. 若将图中所有弧改为边，请分别使用 Prim（从顶点 v3 出发）和 Kruskal 算法找到最小生成树。要求写出详细步骤。

    弧：有向图中连接两个节点的媒介通常叫做“弧”。 边：无向图中连接两个节点的媒介通常叫做“边”。

    • Prim算法：

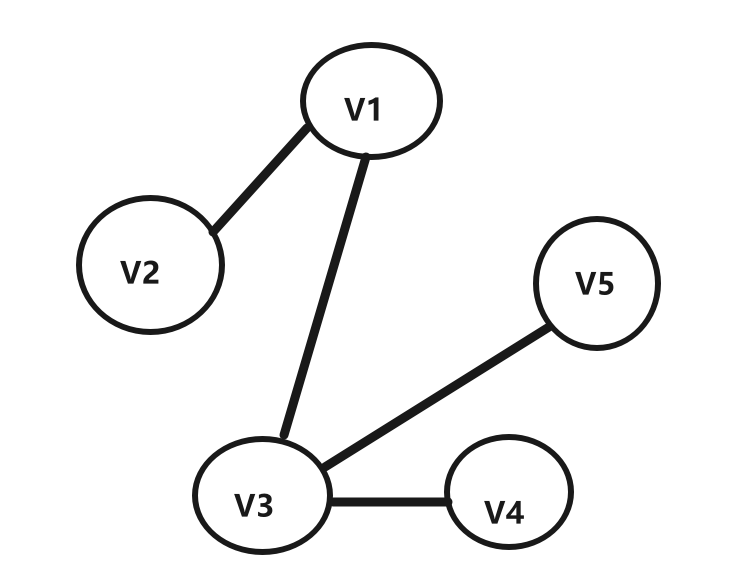
      • 步骤一：以V3为考虑中心，找到与其连接的权值最小的边为10，连接V3与V5构成子图1
      • 步骤二：以子图1为考虑中心，找到与其连接的权值最小的边为20，连接子图1与V4构成子图2
      • 步骤三：以子图2为考虑中心，找到与其连接的权值最小的边为30，连接子图2与V1构成子图3
      • 步骤四：以子图3为考虑中心，找到与其连接的权值最小的边为10，连接子图3与V2，至此，构成最小生成树
      image-20231224191853720

    • Kruskal算法：

      • 步骤一：找到图中权值最小的边为10有两条，这里我们连接V1与V2
      • 步骤二：继续寻找图中剩余没有连接的权值最小的边为10，检验两端节点是否已连通，发现没有连通，连接V3与V5
      • 步骤三：继续寻找图中剩余没有连接的权值最小的边为20，检验两端节点是否已连通，发现没有连通，连接V3与V4
      • 步骤四：继续寻找图中剩余没有连接的权值最小的边为30，检验两端节点是否已连通，发现没有连通，连接V1与V3，至此，构成最小生成树
      image-20231224191853720

  2. 若源点为 V1，请使用 Dijkstra 算法，找出 V1 到其他顶点的最短路径，并逐一写出步骤。

    • 步骤一：构建三个数组并初始化，分别为：

      • final数组，标记个顶点是否已经找到最短路径：final[5]=[1,0,0,0,0]
      • dist数组，记录V0到各顶点的最短路径长度：dist[5]=[0,9999,9999,9999,9999]
      • path数组，记录对应点路径的前驱：path[5]=[-1,-1,-1,-1,-1]

    • 步骤二：遍历V1出度，更改数组的值为：

      • dist[5]=[0,10,30,9999,100]
      • path[5]=[-1,0,0,-1,0]

      找到dist中最小值，认为找到该节点到V1的最短路径，更改final数组为final[5]=[1,1,0,0,0]

    • 步骤三：遍历V2出度，更改数组的值为：

      • dist[5]=[0,10,30,9999,100]

        V2到V3权值为50，10+50>30，故不作修改

      • path[5]=[-1,0,0,-1,0]

      找到dist中最小值，认为找到该节点到V1的最短路径，更改final数组为final[5]=[1,1,1,0,0]

    • 步骤四：遍历V3出度，更改数组的值为：

      • dist[5]=[0,10,30,9999,40]

        V3到V5权值为10，30+10<100，故作修改

      • path[5]=[-1,0,0,-1,2]

      找到dist中最小值，认为找到该节点到V1的最短路径，更改final数组为final[5]=[1,1,1,0,1]

    • 步骤五：遍历V5出度，更改数组的值为：

      • dist[5]=[0,10,30,100,40]

        V5到V4权值为60，40+60<9999，故作修改

      • path[5]=[-1,0,0,4,2]

      找到dist中最小值，认为找到该节点到V1的最短路径，更改final数组为final[5]=[1,1,1,1,1]。至此找到V1到其他全部节点的最短路径，路径值保存在dist中，连接方式保存在path中

  3. 请使用 Floyd 算法，找出有向网各个顶点之间的最短路径，并逐一写出步骤。

    • 步骤一：构建该有向图的邻接矩阵，并且构建一个类似于Dijkstra 算法中的path矩阵，并进行初始化

      • A^0=

        目前来看各顶点间的最短路径长度

        V1 V2 V3 V4 V5
        V1 0 10 30 9999 100
        V2 9999 0 50 9999 9999
        V3 9999 9999 0 9999 10
        V4 9999 9999 20 0 9999
        V5 9999 9999 9999 60 0

      • path^0=

        两个顶点之间的中转点

        V1 V2 V3 V4 V5
        V1 -1 -1 -1 -1 -1
        V2 -1 -1 -1 -1 -1
        V3 -1 -1 -1 -1 -1
        V4 -1 -1 -1 -1 -1
        V5 -1 -1 -1 -1 -1

    • 步骤二：若允许V1作为中转点，遍历每个顶点的出度，若其以V1作为中转点时距离小于A^0中的值，则更改A^1中对应的长度，并且在path^1数组中记录其中转点

      • A^1=

        目前来看各顶点间的最短路径长度

        V1 V2 V3 V4 V5
        V1 0 10 30 9999 100
        V2 9999 0 50 9999 9999
        V3 9999 9999 0 9999 10
        V4 9999 9999 20 0 9999
        V5 9999 9999 9999 60 0

      • path^1=

        两个顶点之间的中转点

        V1 V2 V3 V4 V5
        V1 -1 -1 -1 -1 -1
        V2 -1 -1 -1 -1 -1
        V3 -1 -1 -1 -1 -1
        V4 -1 -1 -1 -1 -1
        V5 -1 -1 -1 -1 -1

    • 步骤三：若允许V2作为中转点，遍历每个顶点的出度，若其以V2作为中转点时距离小于A^1中的值，则更改A^2中对应的长度，并且在path^2数组中记录其中转点

      • A^2=

        目前来看各顶点间的最短路径长度

        V1 V2 V3 V4 V5
        V1 0 10 30 9999 100
        V2 9999 0 50 9999 9999
        V3 9999 9999 0 9999 10
        V4 9999 9999 20 0 9999
        V5 9999 9999 9999 60 0

      • path^2=

        两个顶点之间的中转点

        V1 V2 V3 V4 V5
        V1 -1 -1 -1 -1 -1
        V2 -1 -1 -1 -1 -1
        V3 -1 -1 -1 -1 -1
        V4 -1 -1 -1 -1 -1
        V5 -1 -1 -1 -1 -1

    • 步骤四：若允许V3作为中转点，遍历每个顶点的出度，若其以V3作为中转点时距离小于A^2中的值，则更改A^3中对应的长度，并且在path^3数组中记录其中转点

      • A^3=

        目前来看各顶点间的最短路径长度

        V1 V2 V3 V4 V5
        V1 0 10 30 9999 40
        V2 9999 0 50 9999 60
        V3 9999 9999 0 9999 10
        V4 9999 9999 20 0 30
        V5 9999 9999 9999 60 0

      • path^3=

        两个顶点之间的中转点

        V1 V2 V3 V4 V5
        V1 -1 -1 -1 -1 2
        V2 -1 -1 -1 -1 2
        V3 -1 -1 -1 -1 -1
        V4 -1 -1 -1 -1 2
        V5 -1 -1 -1 -1 -1

    • 步骤五：若允许V4作为中转点，遍历每个顶点的出度，若其以V4作为中转点时距离小于A^3中的值，则更改A^4中对应的长度，并且在path^4数组中记录其中转点

      • A^4=

        目前来看各顶点间的最短路径长度

        V1 V2 V3 V4 V5
        V1 0 10 30 9999 40
        V2 9999 0 50 9999 60
        V3 9999 9999 0 9999 10
        V4 9999 9999 20 0 30
        V5 9999 9999 80 60 0

      • path^4=

        两个顶点之间的中转点

        V1 V2 V3 V4 V5
        V1 -1 -1 -1 -1 2
        V2 -1 -1 -1 -1 2
        V3 -1 -1 -1 -1 -1
        V4 -1 -1 -1 -1 2
        V5 -1 -1 3 -1 -1

    • 步骤六：若允许V5作为中转点，遍历每个顶点的出度，若其以V5作为中转点时距离小于A^4中的值，则更改A^5中对应的长度，并且在path^5数组中记录其中转点

      • A^5=

        目前来看各顶点间的最短路径长度

        V1 V2 V3 V4 V5
        V1 0 10 30 100 40
        V2 9999 0 50 120 60
        V3 9999 9999 0 70 10
        V4 9999 9999 20 0 30
        V5 9999 9999 80 60 0

      • path^5=

        两个顶点之间的中转点

        V1 V2 V3 V4 V5
        V1 -1 -1 -1 4 2
        V2 -1 -1 -1 4 2
        V3 -1 -1 -1 -1 -1
        V4 -1 -1 -1 4 2
        V5 -1 -1 3 -1 -1

      至此，找出了所有向网各个顶点之间的最短路径，A^5记录长度，path^5记录路径