《Distributional Learning for Network Alignment with Global Constraints》
《具有全局约束的网络对齐的分布式学习》

image-20240902231255989

0 摘要

网络对齐，即在源网络和目标网络之间配对对应节点，在许多数据挖掘任务中扮演着重要角色。大量研究集中于在统一空间中学习跨不同网络的节点嵌入。然而，这些方法没有考虑到对齐节点之间的巨大结构差异，因此在很大程度上受到节点确定性表示的限制。在这项工作中，我们提出了一个新的网络对齐框架，以分布学习和全局最优对齐为特色。通过高斯分布对每个节点的不确定性建模，我们的框架基于分布之间的Wasserstein距离构建相似性矩阵，并应用Sinkhorn操作，以端到端的方式学习全局最优映射。我们表明，框架中的每个集成部分都有助于整体性能。在各种实验设置下，我们的对齐框架显示出比最新技术更高的准确性和效率。

关键词：图对齐，分布式学习

1 引言

网络对齐（Network Alignment, NA），即在不同网络之间配对对应节点，同时保留拓扑信息，已经在现实世界的案例中引起了广泛关注。由于网络是许多类型的现实世界数据的自然表示形式，网络对齐技术在许多应用中起着核心作用。应用示例包括但不限于计算机视觉中用于视觉跟踪的2D/3D形状匹配、社交网络的用户去匿名化以及跨语言知识图谱中的实体对齐。

在现有的绝大多数网络对齐方法中，节点是根据确定的节点嵌入进行对齐的。这些方法利用距离度量（例如余弦距离）来对齐欧几里得空间中最接近的邻居，因为它们的拓扑结构最为相似。然而，由于多种实际原因，相同的节点在不同的网络中可能会有较大的结构差异。例如，同一个用户通常在不同的平台上有不同的社交关系，导致在每个网络中的观察不完整。此外，意外或有意的结构扰动会引入虚假的链接并扩大差异。在这些情况下，结构差异将导致嵌入的差异，从而导致次优结果。

我们通过一个示例来更好地解释这一动机。如图1所示，在两个同构网络中，我们有两对锚节点（v3, u3）和（v4, u4）。假设在v2和v3之间插入了一条额外的边（v2, v3），即v2和u2之间出现了一个小的差异。我们用分布 ̃vi 表示每个节点，其中每个维度 ̃vi j 表示从节点 vi 到节点 vj 在单跳内的路径数量。例如， ̃u2 = [1, 0, 0, 2, 0, 0]，u6 = [0, 0, 2, 2, 1, 0]，v ′2 = [1, 0, 2, 2, 0, 0]，其中 v ′2 表示插入后的扰动节点 v2。注意，我们为锚节点 {v3, v4} 和 {u3, u4} 相关的路径赋予了更大的权重 2，因为它们更为重要。为了消除不同路径数量的影响，我们计算了每对节点之间的余弦相似度，并得出 cos (v ′2, u6) > cos (v ′2, u2)。因此，基于确定性嵌入的网络对齐方法会错误地将 v2 与 u6 对齐。例如 Bright 中提到的方法。在现实中，每个节点的嵌入本质上是不确定的，因为现实世界网络的形成和演变充满了不确定性。确定性节点嵌入可以看作是来自潜在分布的样本；因此，差异源于采样的不确定性。捕捉这种不确定性可以提高对网络间结构差异的容忍度，从而增强网络对齐模型的有效性。

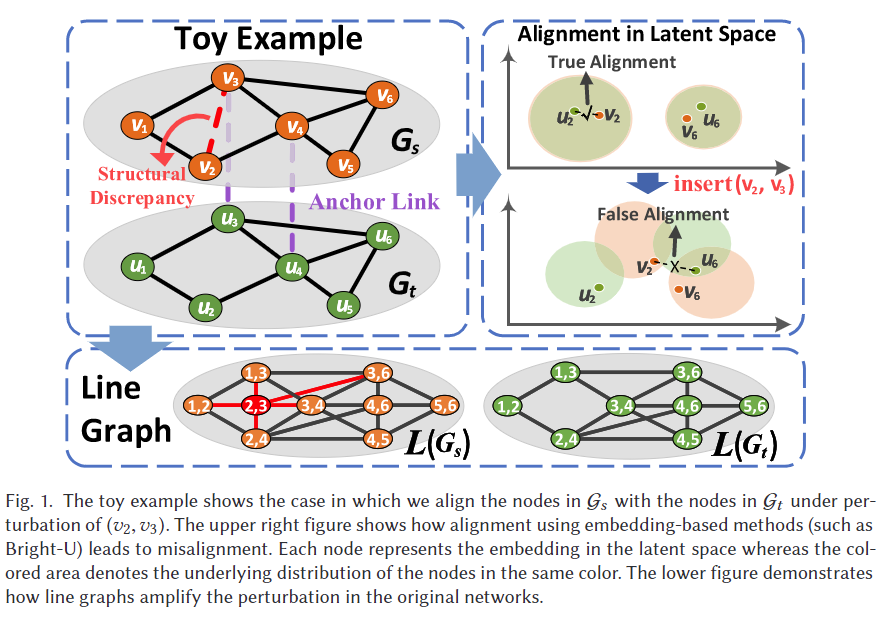
image-20240902091003299

之前的研究通过假设节点嵌入服从高斯分布来建模不确定性，但只考虑了单一网络的重构，而忽略了跨网络对齐的要求，因此，它们通常会产生次优结果。更重要的是，它们忽略了潜在的一对一映射约束，使得目标网络中的每个节点可能会被选为多个源节点的对齐结果。因此，这些方法无法找到全局最优解，其对齐（top-1）的准确率较低。例如，在图1中，在边插入之后，u6 会被错误地对齐到 v2。如果我们施加目标网络中的每个节点只能分配给一个源节点的约束，u2 将被对齐到 v2，而 u6 将由于从全局视角的最短距离而对齐到 v6。很明显，全球对齐约束有助于逃离次优结果，从而提高准确率。然而，全球一对一映射约束通常导致一个NP完全的分配问题，难以在多项式时间内解决。

在本文中，我们提出了一种基于分布学习的网络对齐方法（DLNA），具有全球对齐约束，是一种从全球节点分布视角进行网络对齐的新框架。具体来说，我们假设每个节点服从独立的高斯分布，并在Wasserstein空间中联合学习节点嵌入和受约束（即一对一映射）的网络对齐。考虑到一对一映射是NP完全的，我们使用简化的Sinkhorn算法来逼近这一约束。更重要的是，我们引入了线图来放大网络之间的结构差异，以学习边的嵌入。例如，在图1中，G中的每条边对应于L(G)中的一个节点，而在v2和v3之间插入的边将在相应的线图中围绕v23产生五条额外的边。

我们贡献的亮点如下：

  • 我们引入了一对一映射约束，以获取全局最优对齐。考虑到一对一映射是NP完全的，我们应用简化的Sinkhorn算法来逼近这一约束。
  • 我们提出了一个用于网络对齐和分布学习的联合学习框架DLNA。DLNA利用高斯分布来表示节点，并在分布之间的Wasserstein空间中构建对齐。线图被引入作为增强的特征，以提高不同网络的区分能力。
  • 我们在各种现实世界的数据集上进行了广泛的实验，结果表明DLNA的性能优于现有的技术。

2 相关工作

网络对齐 (NA) 通常被表述为一个优化问题。例如，基于一种假设，即一个网络是另一个网络的噪声置换，一个经典的表述是最小化||A2-P^TA1P||_F^2,其中P是一个置换矩阵。然而，这样的优化问题本质上是NP难的，因为它等价于求解一个二次分配问题。因此，提出了一系列有效的优化方法来解决这个问题。特别是，Zhang和Tong提出了一个优化框架FINAL，利用属性信息来指导基于对齐一致性原则的对齐过程。Du和Tonq基于Krvlov子空间对FINAL进行了加速和扩展。

近年来，提出了许多基于网络嵌入的方法。这些方法都旨在找到合适的节点嵌入，以保持网络内部和网络间的拓扑相似性。例如，IONE提出了一个统一框架，同时解决网络嵌入和对齐任务。Bright 考虑了带有重启的随机游走，以避免基于嵌入方法中的空间差异问题。一些研究试图学习跨属性网络的变换。SNNA结合了度分布和Wasserstein生成对抗网络（WGAN）框架来学习两个网络之间的投影函数。Zhang等人提出了NetTrans，通过图卷积网络（GCN）的分层方式来学习变换。虽然SNNA考虑了网络的分布，但它主要关注网络的全局分布，这难以捕捉，因为它涉及大量节点以及复杂的网络拓扑。UANA提出了一种两阶段的范式，分别在不同阶段学习不确定性感知的节点表示和网络对齐。由于在此过程中忽略了网络对齐对分布学习的影响，因此所学到的嵌入无法很好地捕捉结构差异。

与这些方法相比，我们认为每个节点是从与节点特征、本地结构、跨网络对齐等相关的潜在分布中抽取的，并且在端到端的方式下学习节点表示和网络对齐的不确定性。

3 预备知识与问题定义

3.1 p-Wasserstein 距离

3.1.1 基本概念

p-Wasserstein 距离是一种用来度量两个概率分布之间差异的距离度量。在机器学习、最优传输理论和图像处理等领域，它被广泛应用来比较概率分布。

简单来说，p-Wasserstein 距离考虑的是将一个概率分布(例如一堆沙子)转换成另一个概率分布(另一堆沙子) 所需要的最小代价。这个代价是根据你在空间中"移动”这些概率质量时所消耗的成本来计算的，而这个成本是基于两个点之间的距离(通常是L_p距离)来定义的。

3.1.2 L_{p}距离

在讨论 Wasserstein 距离之前，了解L_p距离是很重要的。L_p距离是一种常见的度量距离的方式，它描述了两个点或向量之间的距离。公式如下：

L_p(x,y)=\left(\sum_{i=1}^n|x_i-y_i|^p\right)^{\frac1p}

  • 当p=1时，L_p距离就是曼哈顿距离。

  • 当p=2时，L_p距离就是欧几里得距离。

  • 当 p 趋向于无穷大 时，L_p 距离变为 切比雪夫距离（Chebyshev distance），计算的是各个分量差值的最大值：

    L_\infty(x,y)=\max_i|x_i-y_i|

3.1.3 p-Wasserstein 距离的定义

p-Wasserstein 距离将L_p距离的概念扩展到概率分布之间。对于两个概率测度 \mu \text{和} v，p-Wasserstein 距离定义为：

W_p(\mu,v)^p=\inf E[d(X-Y)^p],

这个公式可以分解成以下几个部分来理解：

  • X和Y：这是两个随机变量，它们分别服从 \mu \text{和} v这两个概率分布。

  • d(X-Y)：这是X和Y之间的L_p距离，它度量了在空间中将X位置的“质量”移动到Y位置的代价。

    这里X与Y都是向量，所以可以计算他们之间的距离

  • E[d(X-Y)^p]：这是期望值，即我们计算所有可能的移动代价，然后取平均值（期望值）。

  • inf：这是最小值，意味着我们希望找到最小的总代价。我们取了Rn × Rn 上的所有随机向量 (X, Y)，其中 X 服从 μ，Y 服从 υ

因此，p-Wasserstein 距离衡量了将一个分布\mu变换为另一个分布v的最小“运输成本”。

3.1.4 高斯分布情况下的 2-Wasserstein 距离

在高斯分布的情况下，p-Wasserstein 距离有一个特定的闭式解。假设两个概率分布\mu=\mathcal{N}(m_1,\Sigma1)和v=\mathcal{N}(m_2,\Sigma2)是高斯分布，其中m_1和m_2是均值向量，\Sigma1和\Sigma2是协方差矩阵。

这个跟我们的平时见到的普通正太分布还是有一点区别的。

image-20240902220832794

2-Wasserstein 距离的公式如下：

d=W_2^2(N(m1,\Sigma1),N(m2,\Sigma2))=||m1-m2||_2^2+\mathrm{Tr}(\Sigma1+\Sigma2-2(\Sigma1^{1/2}\Sigma2\Sigma1^{1/2})^{1/2}
  • 第一项||m1-m2||_2^2：这是两个高斯分布的均值之间的欧几里得距离的平方，表示两个分布在中心位置上的差异。
  • 第二项\mathrm{Tr}(\Sigma1+\Sigma2-2(\Sigma1^{1/2}\Sigma2\Sigma1^{1/2})^{1/2})：这是协方差矩阵之间的差异，表示两个分布在形状和扩展上的差异。

3.1.5 对角协方差矩阵的简化

在本文中，假设协方差矩阵是对角形式（即矩阵中的非对角元素为0），公式可以进一步简化为：

d=||m1-m2||_2^2+||\Sigma1^{1/2}-\Sigma2^{1/2}||_F^2
  • 第一项||m1-m2||_2^2没有改变，依旧是均值之间的距离。
  • 第二项||\Sigma1^{1/2}-\Sigma2^{1/2}||_F^2是两个对角协方差矩阵的 Frobenius 范数的平方，它度量了协方差矩阵之间的差异。

3.2 线图

假设 G = (V, E) 是一个有限的无向图。我们用 L(G) = (VL, EL) 表示 G 的线图，即 L(G) 的顶点是 G 的边，如果 G 的两条边相邻，那么 L(G) 的两个顶点也相邻。图1中展示了示例构造。关联矩阵 H ∈ R|V|×|VL| 建立了 L(G) 与 G 之间的对应关系，其中 H(v, vL) 的定义如下：

H(v,vL)=\begin{cases}1,&\text{如果 v 属于 L(G) 中的边 }e(vL)\\0,&\text{否则}\end{cases}

3.3 问题定义

设 Gs = (Vs, Es, Xs^a)，Gt = (Vt, Et, Xt^a) 分别为源网络和目标网络。每个网络由一组有限的节点 V = {v1, ... , v|V|}，一组有限的边 E = {eij}，以及一个可选的节点特征矩阵 X^a ∈ R|V|×· 组成。我们将已知的一组配对锚点节点集表示为 L = {(vs1, vt1), ... , (vsn, vtn)}。

网络对齐问题定义如下：给定源网络 Gs 和目标网络 Gt 以及锚点链接集 L，我们的目标是学习一个映射矩阵 SM ∈ {0, 1}|Vs|×|Vt|。最终，SM 推断出一个注射映射函数 π : Vs → Vt，将 Gs 中的每个节点映射到 Gt 中的一个节点。

4 提出的框架

动机：

我们提出了一个网络对齐（NA）框架，该框架不是直接对齐节点本身，而是通过一对一映射约束来全局对齐源节点和目标节点的分布。直观地讲，全局对齐分布可以容忍观察节点的潜在结构差异，从而帮助揭示网络之间的真实对齐。

在现实中，不同网络中的相同节点通常具有不同的结构或属性，因此不适合进行精确的嵌入。局部对齐会进一步增加误差，因为每个目标节点可能会被对齐到多个源节点。我们还引入了线图作为另一种特征，以放大错配中的差异。

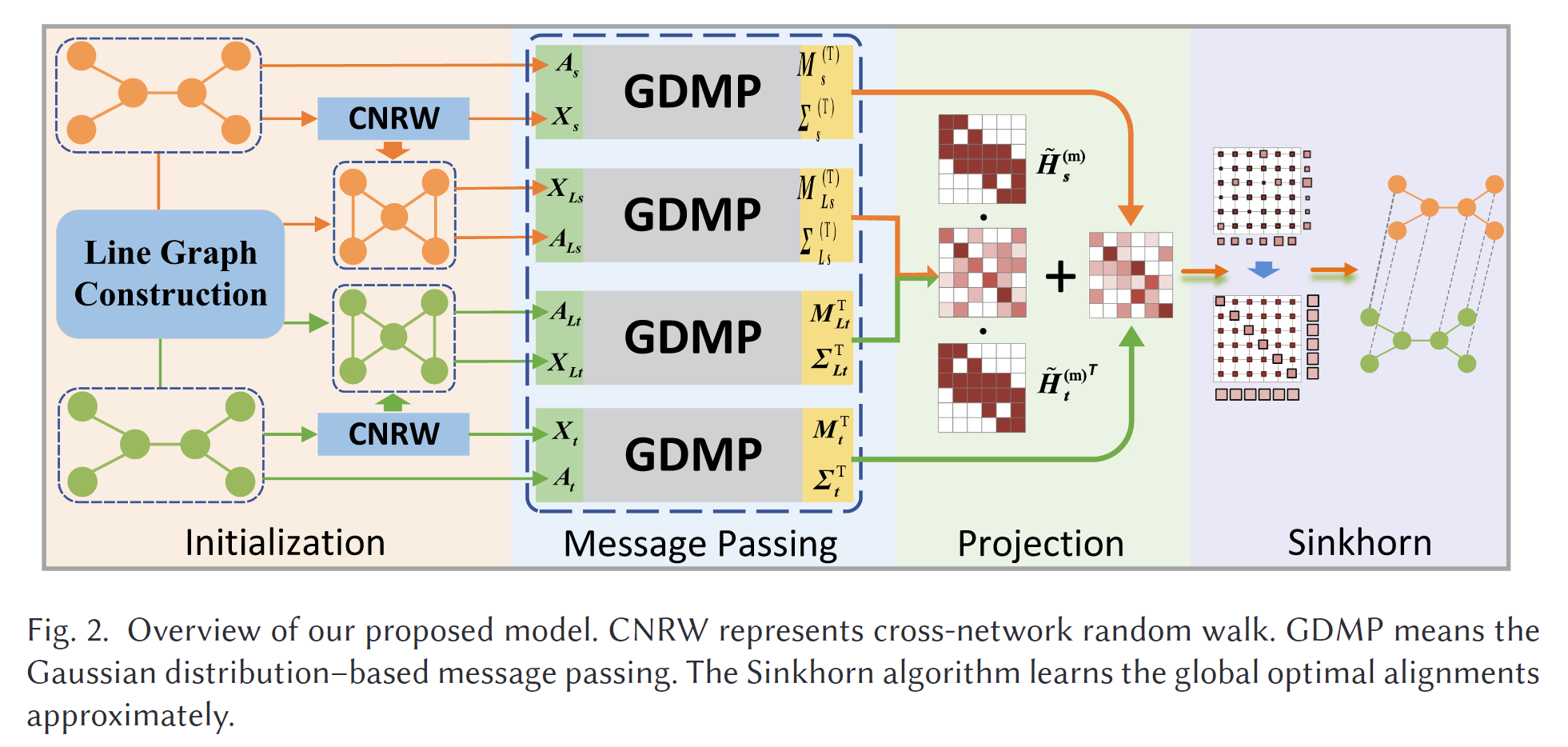
该框架的示意图如图2所示。

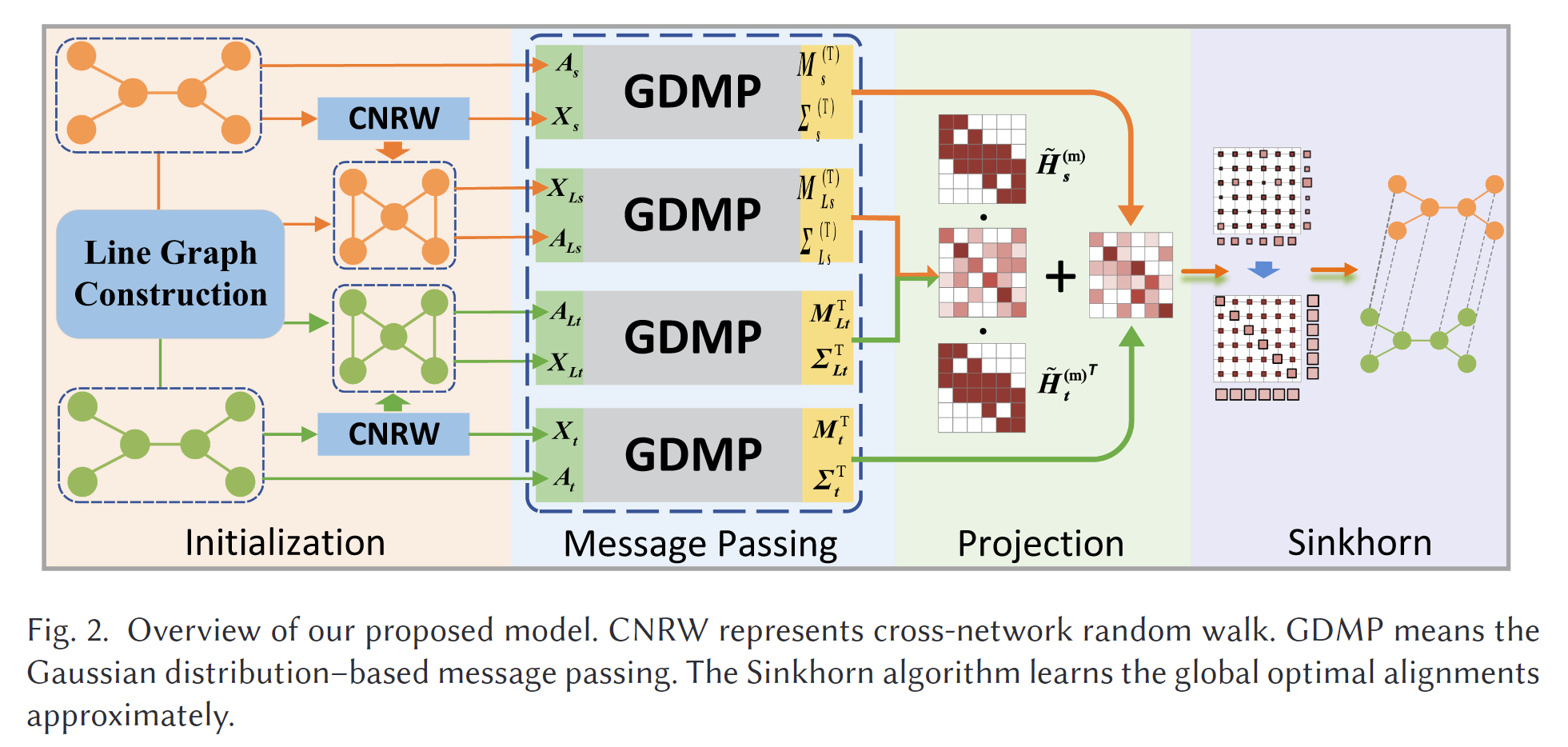
image-20240902231249934

  1. 我们使用基于随机游走的方法来初始化网络嵌入，并构建原始网络的线图。
  2. 假设每个节点的特征服从高斯分布，我们学习这些分布并利用消息传递机制聚合分布级邻域信息。
  3. 最后，我们通过Wasserstein度量计算相似度矩阵，并执行Sinkhorn操作，以找到全局最优的节点分布对齐解决方案。在接下来的部分中，我们将详细介绍我们的框架。

image-20240902230350177

4.1 跨网络随机游走

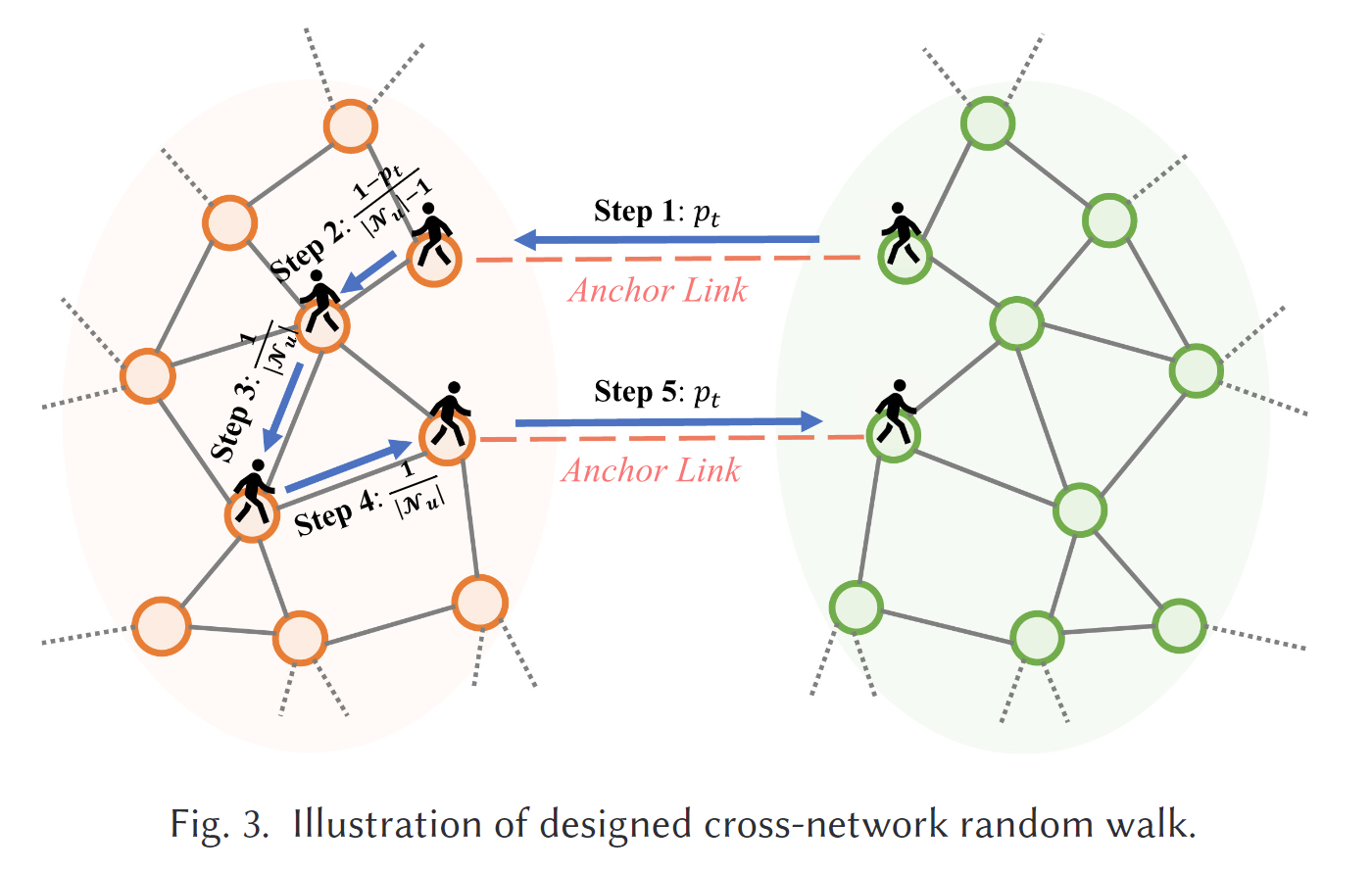
image-20240902233540374

对于没有属性的网络，只给定源网络和目标网络的邻接矩阵 A_s 和 A_t，以及锚节点对的对应集 L。我们应用跨网络随机游走（见图3）和 Skip-gram 算法，在初始化步骤中为两个网络构建一个统一的嵌入空间。具体来说，我们通过虚拟边将源网络和目标网络中的每对锚节点连接起来，以构建一个新的网络 G' = {V', E'}，其中 V' = V_s ∪ V_t 和 E' = E_s ∪ E_t ∪ L。然后，我们在 G' 上按照以下转移概率进行随机游走：

p(v|u)=\begin{cases}p_t,&\text{如果}v=\pi(u)\\\frac{1-p_t}{|N(u)|-1},&\text{如果}\pi(u)\in N(u)\text{且}v\neq\pi(u)\\\frac{1}{|N(u)|},&\text{其他情况下}\end{cases}

其中 N(u) 表示节点 u 的邻居，|N(u)| 是邻居的数量，p_t 表示源网络和目标网络中锚节点之间的转移概率。根据文献 [16]，我们采用 Skip-gram 算法，通过最大化应用负采样的随机游走序列的似然来学习节点的嵌入。因此，我们分别为 G_s 和 G_t 获得了初始化的节点嵌入 X_s = {u_{s1}, u_{s2}, \dots, u_{s|V_s|}} 和 X_t = {u_{t1}, u_{t2}, \dots, u_{t|V_t|}}。如果 G_s 和 G_t 是具有属性的网络，并且给出了输入特征矩阵 X^a，我们设置 X = X || X^a。

||表示拼接操作

定理1：如果 p_t = \frac{c}{|N(u)| - 1 + c}，其中 c > 1，设计的随机游走可以收敛到稳态分布。

证明：我们将源图和目标图之间的边赋予权重 c，其他边赋予权重 1 在 G' 上。因此，我们得到加权邻接矩阵 W，使得 W_{ij} = c 当 v_j = \pi(v_i)，否则 W_{ij} = 1。设对角度矩阵 D 的对角元素为 d_{ii} = \sum_j W_{ij}。因此，转移矩阵 P = D^{-1}W。考虑对称矩阵 N = D^{-1/2}WD^{-1/2} = D^{1/2}PD^{-1/2}，它可以写成谱形式：N = \sum_{k=1}^n \lambda_k v_k v_k^T。我们可以很容易地得到特征向量 z = {\sqrt{D_{11}}, \dots, \sqrt{D_{nn}}}，因为 N z = D^{-1/2}W 1 = D^{-1/2}z 2 = 1z。由于特征向量 z 是与特征值1对应的正特征向量，按照 Frobenius-Perron 定理，我们有 \lambda_1 = 1 > \lambda_2 \geq \dots \geq \lambda_n \geq -1，且 v_{1i} = \sqrt{D_{ii}} / \sum_k D_{kk}。现在，我们有 P^m = D^{-1/2}N D^{1/2} = Q + \sum_{k=2}^n \lambda_k^m D^{-1/2}v_k v_k^T D^{1/2} 经过 m 次转移，其中 Q_{ij} = \frac{D_{jj}}{\sum_k D_{kk}}。如果 G' 不是二部图，则对于 k = 2, \dots, n，\lambda_k < 1，且当 m \to \infty 时，p_{ij}^m \to \frac{D_{jj}}{\sum_k D_{kk}}，因此我们的随机游走收敛到稳态分布 s(i) = \frac{D_{ii}}{\sum_k D_{kk}}。

4.2 线图构建

为了捕捉高阶信息并放大网络之间的差异，我们在学习框架中引入了线图。给定一个网络 G，我们将其线图定义为 L(G) = (V_L, E_L, A_L, X_L)。其中，A_L 和 X_L 分别是 L(G) 的邻接矩阵和特征矩阵，它们可以通过以下方程构建：

x_{L,i}=\bigoplus_{j}H_{ij}x_{j}\\A_{L}=H^{T}H-2I

其中，\bigoplus 是连接非零向量的操作。通过上述操作，我们可以轻松地使用在 G 上执行的相同方法学习 L(G) 中节点（即 G 中的边）的隐藏状态。这种表示描述了原始网络中边的相似性，有助于从边的角度改进对齐。

原始图的关联矩阵 H：假设图 G 的关联矩阵是 H，其中 H_{ij} = 1 表示节点 v_i 与边 e_j 关联，即 v_i 是 e_j 的一个端点，其他情况下 H_{ij} = 0。

线图的邻接矩阵 A_L 构建中：H^T 是 H 的转置矩阵，I 是单位矩阵。这个公式的含义是，矩阵 H^T H 给出了原始图中共享一个公共节点的边的关系，而减去 2I 则是去掉自环，因为每条边在 H^T H 中与自己共享了两个节点。

特征矩阵构建中：对于线图中的节点（即原始图的边），它的特征可以通过将与其关联的原始图节点的特征拼接在一起构成。其中，\bigoplus 表示将与边 e_i 相关联的所有节点的特征向量进行拼接。

4.3 基于高斯的分布学习

在源网络和目标网络及其线图上，我们的目标是学习各自节点的潜在分布。为了简化讨论，我们以网络 G 为例，它可以表示源网络、目标网络、源网络的线图或目标网络的线图，如图 4 所示。

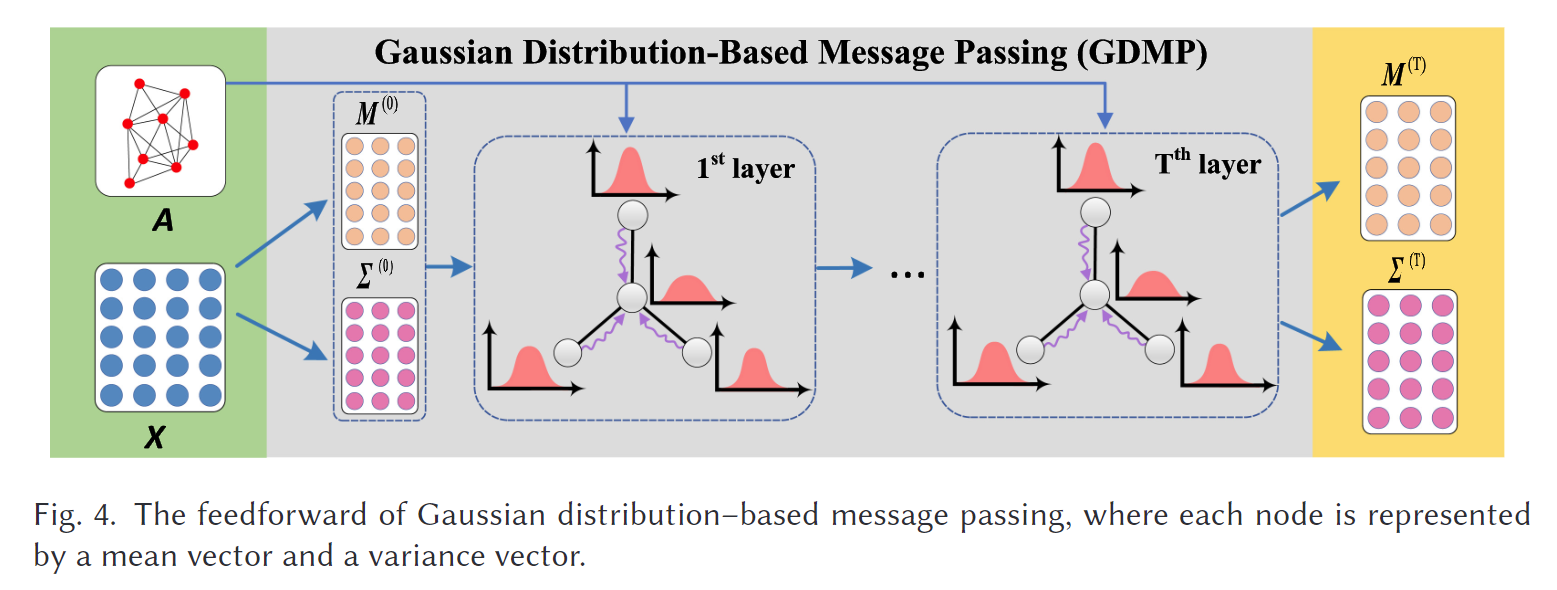image-20240903001039269我们假设每个节点的潜在状态（由学习到的特征表示)服从多元高斯分布，即：

h_i\sim\mathcal{N}(m_i,\mathrm{diag}(\sigma_i^2))

其中，m_i 是第 i 个节点的均值向量，\text{diag}(\sigma_i^2) 是第 i 个节点的对角方差矩阵，\forall i \in {1, \dots, n}。对于图上的所有节点，我们可以将它们分别表示为 M = {m_1, m_2, \dots, m_n} 和 \Sigma = {\sigma_1^2, \sigma_2^2, \dots, \sigma_n^2}。

然而，推导每个节点的精确高斯分布是不可行的；因此，我们使用==两个前馈神经网络==来学习 M 和 \Sigma，该方法遵循之前的研究 12。具体来说，我们学习以下多元潜在分布：

M^{(0)}=\sigma(XW_m^{(0)}),\quad\Sigma^{(0)}=\sigma(XW_\sigma^{(0)})

这里的 M^{(0)} 和 \Sigma^{(0)} 分别表示第 0 层或输入层的结果，W 是调整后的权重矩阵，\sigma(\cdot) 是非线性激活函数。

显然，配对的节点很可能来自相同的分布；否则，它们的分布将会相距较远。同样，对于线图来说，配对的节点表示原始网络中的对齐边，因此也应来自相同的分布。此外，对齐的节点通常具有相似的邻域。为了捕捉这种结构相似性，我们使用消息传递机制来聚合节点在其邻域中的分布，如文献 33 所述。

假设节点的隐藏表示是独立的，那么在第 t 层的聚合过程如下：

\hat{h}_{i}^{(t+1)}=\sum_{j\in N(i)}\frac{1}{\sqrt{\tilde{D}_{ii}\tilde{D}_{jj}}}h_{j}^{(t)}\sim\mathcal{N}\left(\sum_{j\in N(i)}\frac{1}{\sqrt{\tilde{D}_{ii}\tilde{D}_{jj}}}m_{j}^{(t)},\mathrm{diag}\left(\sum_{j\in N(i)}\frac{1}{\tilde{D}_{ii}\tilde{D}_{jj}}(\sigma_{j}^{(t)})^{2}\right)\right)

很容易证明，方程 (6) 中的 \hat{h}_i^{(t+1)} 也服从高斯分布，因为所有的高斯变量 h_j^{(t)} 都是独立的。然后，我们对 \hat{h}_i^{(t+1)} 应用线性和非线性变换，以获得 h_i^{(t+1)}。

因此，图 G 上节点的分布聚合定义为：

M^{(t+1)}=\sigma(\bar{D}^{-1/2}\bar{A}\bar{D}^{-1/2}M^{(t)}W_{m}^{(t)}),\quad\Sigma^{(t+1)}=\sigma(\bar{D}^{-1}\bar{A}\bar{D}^{-1}\Sigma^{(t)}W_{\sigma}^{(t)})

其中 \tilde{A} = A + I，\tilde{D} 是 \tilde{A} 的对角矩阵，\tilde{D}*{ii} = 1 + \sum_j A*{ij}。对于线图 L(G)，M_L^{(t+1)} 和 \Sigma_L^{(t+1)} 可以以相同的方式获得。

4.4 全局分布映射矩阵

基于每个节点的分布表示，我们的目标是学习跨网络的映射矩阵 SM。我们使用 2-Wasserstein 距离来衡量分布之间的距离。给定两个节点 v_i \in V_s 和 v_j \in V_t 及其在第 T 层的输出 h_i^{(T)} 和 h_j^{(T)}，它们之间的 2-Wasserstein 距离为：

d(h_i^{(T)},h_j^{(T)})=||m_i^{(T)}-m_j^{(T)}||_2^2+||\sigma_i^{(T)}-\sigma_j^{(T)}||_2^2\quad(8)

令 D_{w,ij} = d(h_i^{(T)}, h_j^{(T)})，我们将每对节点之间的 Wasserstein 距离表示为矩阵 D_w，从而定义源网络 G_s 和目标网络 G_t 之间的相似度矩阵为：

S_G=-D_w\quad(9)

同样地，我们定义源网络的线图 L(G_s) 和目标网络的线图 L(G_t) 之间的相似度矩阵为：

S_L^{\prime}=-D_w^{\prime}\quad(10)

其中 D'*{w,ij} 表示 v_i \in V*{L_s} 和 v_j \in V_{L_t} 之间的 2-Wasserstein 距离。尽管由于缺乏边对齐的真实标签，我们无法直接优化 S'_L，但我们将相似度投影到节点上：

S_L=\tilde{H}_sS_L^{\prime}\tilde{H}_t^T\quad(11)

其中 \tilde{H} = D^{-1}H，D 是对角矩阵，其对角线元素 D_{ii} = \sum_j H_{ij}。直觉上，这意味着节点的相似度可以表示为其连接的边的平均相似度得分，即：

S_{L,ij}=\sum_{c_{m},c_{n}}\frac{1}{|N(v_{i})||N(v_{j})|}S_{L,mn}^{\prime}

其中 e_m 和 e_n 是分别连接到 v_i 和 v_j 的边。

结合 S_G 和 S_L，相似度矩阵 S 定义为：

S=\exp(\alpha S_G+(1-\alpha)S_L)\quad(12)

其中指数函数确保所有元素为正数，且 \alpha 是控制 S_G 和 S_L 之间平衡的常数。

为了捕捉输入数据的信息，我们还通过将 S_G^E = X_s X_t^T 和 S_L^E = \tilde{H_s} X_{L_s} X_{L_t}^T \tilde{H_t}^T 包含在优化目标中来考虑节点的相似度：

S=\exp(\alpha(S_G+S_G^E)+(1-\alpha)(S_L+S_L^E))\quad(13)

给定相似度矩阵，我们采用 Sinkhorn 算法（其实很简单，就是一个行列归一化算法）通过将置换矩阵放松为双随机矩阵（即每行和每列的和都为1的矩阵）来学习全局最优的映射。注意，Sinkhorn 算法在方阵上执行，如果 G_s 和 G_t 的节点数量不同，则应填充虚拟行或列。

由于这是一个迭代算法，我们令 S_k 表示第 k 次迭代的结果。我们在每次迭代中执行 Sinkhorn 操作：

S_{k}^{\prime}=S_{k-1}\oslash(S_{k-1}11^{T})\quad(14)\\S_{k}=S_{k}^{\prime}\oslash(11^{T}S_{k}^{\prime})\quad(15)

其中 \oslash 表示按元素除法。通过交替执行方程（14）和方程（15）直到收敛，我们获得了映射矩阵 SM = \text{Sinkhorn}(S)。由于 Sinkhorn 操作是完全可微的，因此整个框架可以端到端地训练。在迭代的 Sinkhorn 操作过程中，模型权重会根据分布相似度以及节点相似度进行更新。

4.5 模型训练

在前述方法中得到的映射矩阵 SM_{ij} 表示节点 i 与节点 j 对齐的概率，交叉熵损失被用作训练的目标函数：

L_1=-\sum_{i\in V_s,j\in V_t}S_{\mathrm{gt},M_{ij}}\log(SM_{ij})\quad(16)

其中，当且仅当节点 i \in G_s 有真实的对应节点 j \in G_t 时，S_{\text{gt}, M_{ij}} = 1。

由于神经网络对每个数据点的输出是确定性的，\sigma 通常会收敛到零，这违背了我们的假设。为了避免方差收敛到零，并确保 h_i 和 h_{L,i} 在训练过程中遵循高斯分布，我们对方程（5）中的潜在表示进行正则化处理：

L_{2}=\sum_{\mathrm{d}\in\{s,t,L_{s},L_{t}\}}\sum_{i\in V_{0}}\mathrm{KL}\left(\mathcal{N}(m_{\mathrm{d},i}^{(0)},\mathrm{diag}((\sigma_{\mathrm{d},i}^{(0)})^{2}))\mid\mid\mathcal{N}(0,I)\right)\quad(17)

其中，\text{KL}(\cdot || \cdot) 是两个分布之间的 KL 散度，m_{\text{d},i} 对应于方程（8）中的 m_i，\text{d} 确定了节点所属的网络。注意，我们只需要对第一层进行正则化，因为在聚合过程中（通过缩放和加性属性），较深的层次已经保证了服从高斯分布。

最终的损失函数为：

L=L_1+\gamma L_2\quad(18)

其中，\gamma 是控制正则化影响的超参数。

总结来说，分布式学习与传统的点对点学习的不同之处在于：特征被分为两部分，一部分代表节点的不确定性，KL 散度的正则化项确保了特征遵循高斯分布。

4.6 可扩展性优化

边采样：对于一个完整的线图 L(G)，它有 |E| 个节点，并且最多有 (d_{\text{max}} - 1)|E| 条边，其中 d_{\text{max}} 是图 G 的最大度。使用所有的边会消耗大量内存，而且在实际中是不现实的。因此，在构建 L(G) 的过程中，我们随机选择 v 在 G 中的 min{|N(v)|, \beta} 个邻居来保留 v 与这些邻居之间的边。需要注意的是，与锚节点相关的任何信息都不会删除，因为它们的边信息在训练中至关重要。

稀疏对应：存储矩阵 S_G \in \mathbb{R}^{|V_s| \times |V_t|}、S_L \in \mathbb{R}^{|V_{L_s}| \times |V_{L_t}|} 和 S \in \mathbb{R}^{|V_s| \times |V_t|} 的完整版本会消耗大量内存。我们首先将 S_G + S_{GE} 和 S_L + S_{LE} 表示为矩阵乘法的形式来计算方程（13）。具体来说，S_G + S_{GE} 可以等效地表示为 S_G + S_{GE} = O_s O_t^T，其中

O_{s}=\mathrm{concat}(X_{s},2M_{s}^{(T)},\Sigma_{s}^{(T)},p_{s},c_{s},-1,-1),\\O_{t}=\mathrm{concat}(X_{t},M_{t}^{(T)},2\Sigma_{t}^{(T)},-1,-1,p_{t},c_{t}),

其中，p 和 c 是两个列向量，p_i = ||m_i^{(T)}||*2^2，c_i = ||\sigma_i^{(T)}||_2^2，而 1 是一个所有元素都为 1 的列向量。我们用相同的方式表示 S_L + S_{LE} = \tilde{H}_s O_{L_s} O*{L_t}^T \tilde{H}_t^T。注意，\tilde{H}_s 和 \tilde{H}_t 是非常稀疏的矩阵。方程（13）的最终表达式为

S=\exp([\alpha O_s||(1-\alpha)\tilde{H}_sO_{Ls}][O_t||\tilde{H}_tO_{Lt}]^T),

其中 || 表示连接操作。此外，如文献[7]中所述，我们可以通过使用 KEOPS 库计算 top-k 对应关系，而不存储其稠密版本，从而高效地稀疏化 S。通过这些方法，我们将所需的内存占用从 |V_s||V_t| 降低到 k|V_s|。具体而言，我们计算每一行 S_{i,:} 的 top-k 对应关系，并存储其稀疏版本，包括真实值的条目 S_{i,\pi(i)}。随后，Sinkhorn 操作在稀疏形式上进行，以逼近 S_M。

4.7 复杂度分析

给定随机游走的数量 \gamma、游走长度 t、窗口大小 w 和表示大小 F，设计的随机游走的时间复杂度为 O(\gamma |V|tw(F + F \log |V|))，与 DeepWalk 算法类似，并且可以高度并行化。对于前向传播，DLNA 其他部分的时间复杂度为 O(l |V| \beta^2 F F' + k |V| F'^2)，其中 l 是 GCN 层的数量，\beta 表示采样图中的最大度，k 是 top-k 稀疏化的参数，F' 是输出表示的大小。DLNA 的空间复杂度为 O(|V|(\beta F' + k + F))。由于所有基准方法的空间复杂度为 O(|V|^2)，DLNA 的空间消耗更少。FINAL 是最有效的基准方法，因为它具有封闭形式的解决方案，时间复杂度为 O(|V|^2 r^4 + F |V|^2)。BRIGHT 是第二高效的基准方法，时间复杂度为 O(|V||L|(lF' + |U_l|) + l |E| F F' + |E| |L|)，高于 DLNA。

5 评估

5.1 实验设置

5.1.1 数据集和评估指标

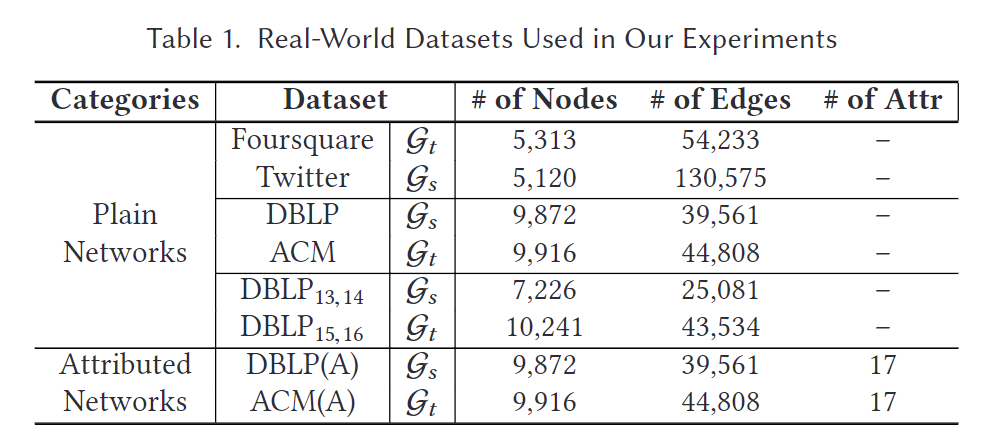
我们的数据集包括：

  1. Twitter-Foursquare：这两个社交网络的数据分别来自Foursquare和Twitter【27】。这两个网络共享1609名用户，作为对齐的真实值。
  2. DBLP-ACM：两个无向共著网络ACM和DBLP分别从四个领域（DM、ML、DB和IR）的论文及其引用信息中提取【17】。每个节点代表一位作者，两节点之间的边表示在至少一篇论文上的合作。两个网络共享6325名作者，作为真实值。此外，每位作者在17个会议上发表的论文数量作为属性数据集，记为DBLP(A)-ACM(A)。
  3. DBLP13,14-DBLP15,16：这两个共著网络分别构建于2013至2014年和2015至2016年在人工智能（AI）会议上发表的论文中。两个网络共享2861名用户，作为真实值。

所有数据集的统计信息列在表1中。我们对所有方法统一数据分割，随机选择所有真实值数据的20%作为训练数据，剩余的80%作为测试数据。

image-20240903165135884

与大多数研究【22, 31】一样，我们采用匹配性能指标Hit@k，它衡量了在前k个对齐结果中正确匹配的对数的比例。

5.1.2 基准方法

我们将我们的方法与八种最先进的方法进行了比较。由于某些方法专门针对非属性网络设计，我们将基准方法分为两组：

  1. 非属性网络：IONE【14】是一个同时解决网络嵌入和用户匹配的半监督模型。FINAL-P是FINAL【28】的非属性版本，利用拓扑一致性来优化对齐矩阵。DeepLink【31】采用随机游走和双重学习来完成对齐任务。CrossMNA【2】是一个多网络对齐模型，保留了跨网络的拓扑信息。CENALP-U是CENALP【6】的非属性版本，在联合学习框架中学习网络对齐和链接预测。PSML-I是基于IONE的PSML【23】模型，仔细植入了伪锚点。BRIGHT-U是BRIGHT【22】的非属性版本，通过重新启动的随机游走构建了一个对齐的统一空间。UANA【30】考虑了节点的不确定性。
  2. 属性网络：REGAL【9】是一种基于跨网络相似性矩阵分解的无监督方法，我们通过利用已知的锚点链接将其扩展到半监督设置。FINAL-N是FINAL【28】的属性版本，额外考虑了属性一致性。SNNA【13】将度分布纳入WGAN框架中，学习源网络和目标网络之间的映射。CENALP-A是CENALP【6】的属性版本。NetTrans【29】使用分层GCN来学习跨网络的投影。PSML-S是基于SNNA的PSML模型，结合了植入的伪锚点。BRIGHT-U是BRIGHT【22】的属性版本，使用GCN来利用属性信息。

5.1.3 超参数

我们框架中的超参数设置如下：p_t = 0.5, \alpha = 0.5, \beta = 10, T = 1, top-k = 500, 对所有数据集进行3次Sinkhorn操作。非线性激活函数对均值使用ELU(·)【3】，对方差使用ReLU(·)【15】，因为方差要求非负。我们将dropout率设为0.2。节点嵌入和隐藏状态的维度分别设为128和100。使用Adam【11】优化器，学习率设为0.0005，权重衰减设为0.0005，在所有数据集上训练50个epoch。对于基准方法，我们采用其开源代码中的默认参数。所有实验均在NVIDIA 2080Ti GPU、Intel(R) Xeon(R) CPU E5-2650 v3 @ 2.30 GHz和256 GB RAM上完成。

5.2 效果和消融研究

5.2.1 在普通网络上的对齐

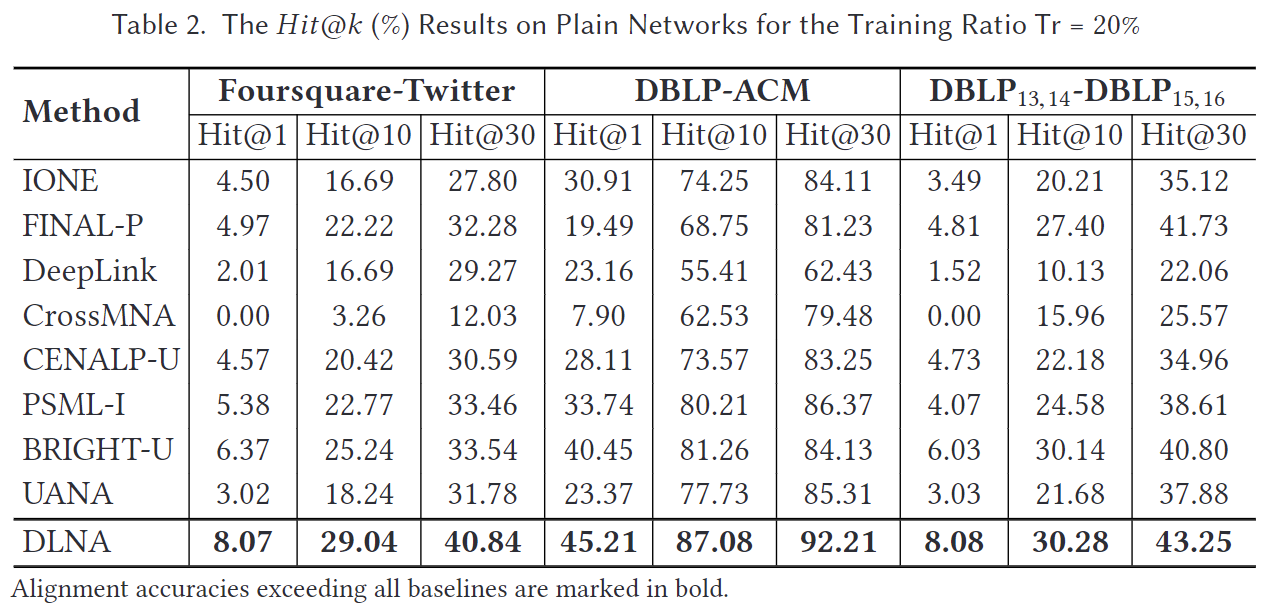
我们在三个数据集上将我们的方法与五个基线进行了比较，结果如表2所示。我们观察到，FINAL-P在Hit@30上的结果与BRIGHT-U相当，这证明了拓扑一致性的有效性。我们提出的方法在各个方面都优于所有基线，特别是在Foursquare-Twitter数据集上，Hit@1提升了3%，Hit@30提升了18%，这表明我们的方法在优化基础方法上具有优势。与最佳的基于嵌入的方法BRIGHT-U相比，DLNA在DBLP-ACM数据集上Hit@1提升了5%，Hit@30提升了8%。

image-20240903171457970

5.2.2 在带属性网络上的对齐

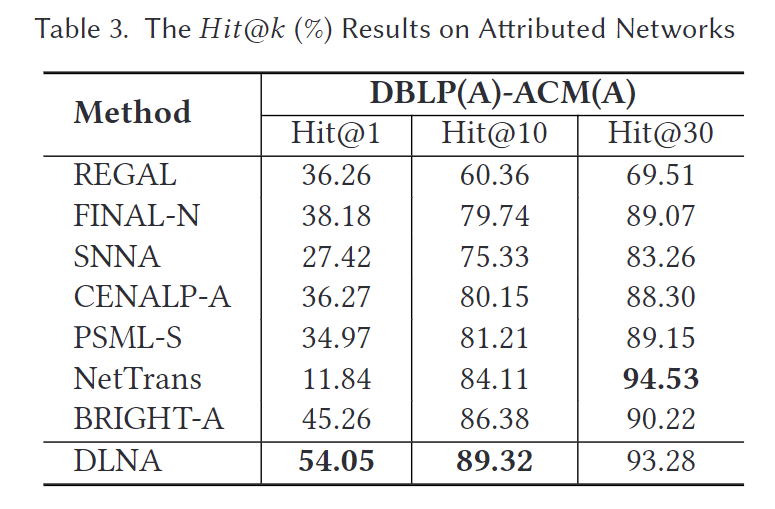
我们在一个带属性的数据集上将我们的方法与七个基线进行了比较，结果如表3所示。虽然BRIGHT-A在Hit@1和Hit@10上优于其他所有基线，但我们的方法在Hit@1上比BRIGHT-A提高了9%，在Hit@10上提高了3%。尽管NetTrans在Hit@30上表现最佳，比DLNA高出1.3%，但DLNA在Hit@1上具有显著优势，约为43%。总之，我们提出的方法在普通网络和带属性网络上均明显优于最新的技术。

image-20240903171640195

5.2.3 消融研究

为了证明我们引入的组件确实有益，我们通过在表4中移除相应部分，将我们提出的方法与不同的变体进行了比较。当舍弃分布学习时，我们将图2中的GDMP部分替换为传统的GCNs。在这种情况下，每一层的隐藏状态是确定性的特征，而不是高斯分布的均值和方差向量，并且两个节点之间的相似性表示为它们最终输出嵌入的内积。为了移除正则化项，将参数γ设置为0。当舍弃Sinkhorn操作时，我们用SM = softmax(S)替换它。当移除线图时，我们将参数α设置为1，以排除公式(12)中的线图。

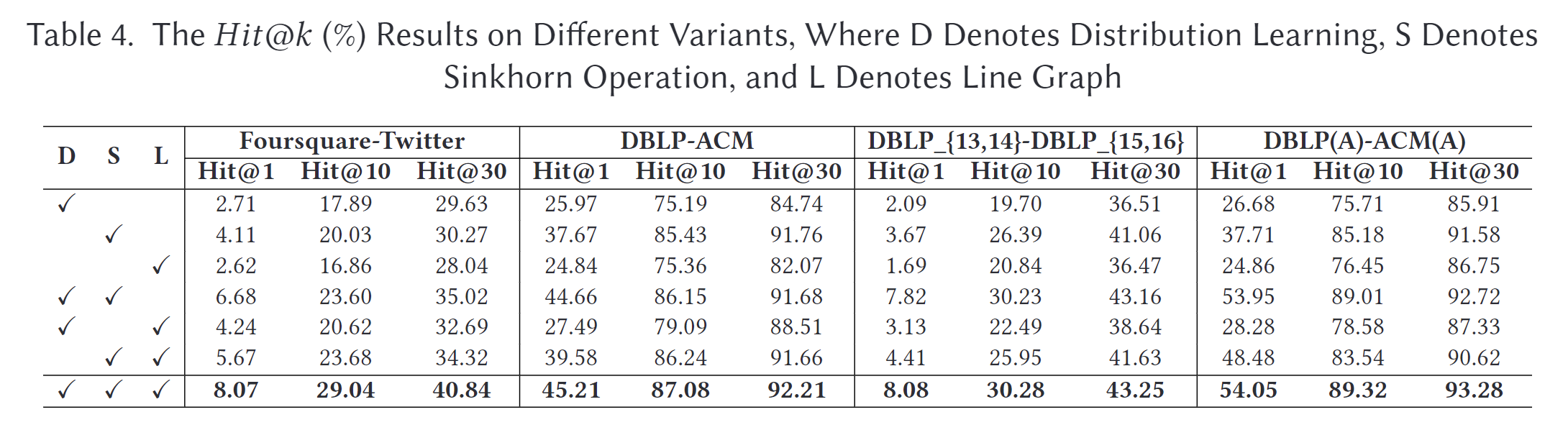
image-20240903171833271

根据结果可以看到，所有变体在所有数据集上的表现都不如DLNA。具体来说，结合Sinkhorn操作总能带来显著的性能提升，这表明通过Wasserstein度量寻找全局最优对齐比选择最近邻更为有效。去除分布学习部分的变体也不如DLNA，这证明了对每个节点的不确定性建模能够找到更好的对齐解决方案。去除线图的变体在Foursquare-Twitter上的准确率明显下降，主要是因为Twitter和Foursquare网络差异很大，而放大这些差异对于更好的对齐至关重要。整体结果表明，DLNA的所有组件在提高对齐性能方面都是有效的。

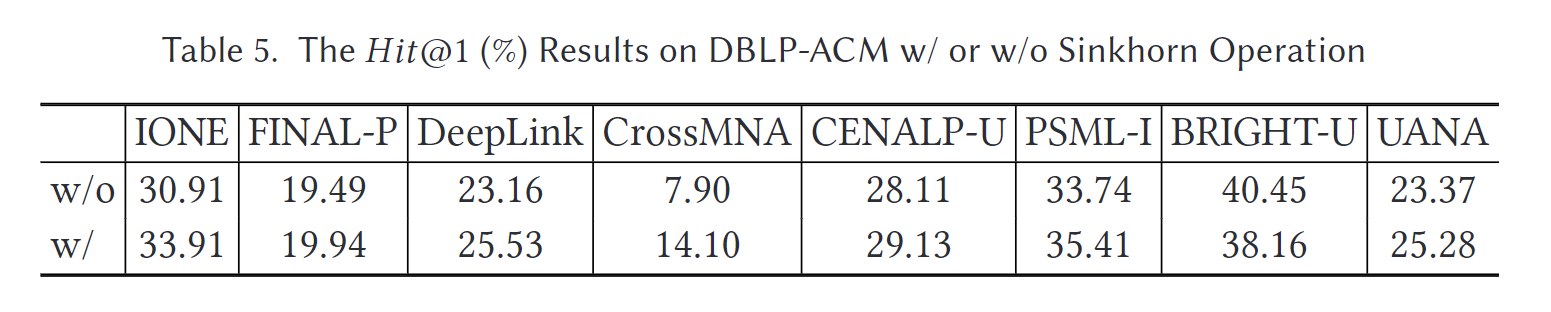
由于Sinkhorn算法可以在任何非负方阵上执行，我们还展示了带有和不带有Sinkhorn操作的DBLP-ACM数据集上的基线结果。具体来说，我们根据所有基线的最终输出嵌入计算相似度矩阵，并添加虚拟行以完成方阵。如表5所示，大多数方法都可以通过Sinkhorn操作得到提升。然而，由于它们在训练中未包含Sinkhorn，因此未能获得与我们的方法相同的收益。

image-20240903172152709

5.3 超参数和效率分析

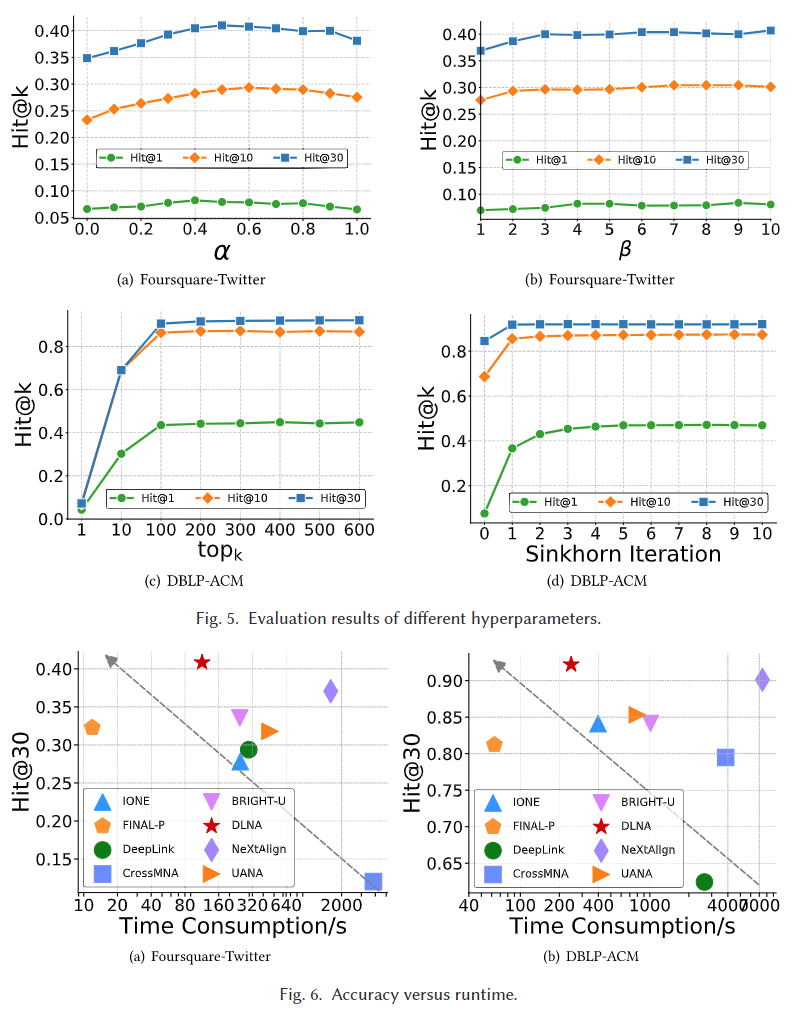
我们研究了对齐准确度对超参数 α、β、topk 和 Sinkhorn 迭代次数的敏感性。我们在 Foursquare-Twitter 数据集上报告了 α、β 的结果，并在 DBLP-ACM 数据集上报告了 topk 和 Sinkhorn 迭代次数的结果。DLNA 的性能变化如图 5 所示。正如我们所看到的，DLNA 在选择 α 约为 0.5 时表现最佳，这表明节点对齐和边对齐都很重要，特别是对于密集网络来说，边对齐更为重要。至于 β，随着 β 的增加，DLNA 获得了稳定的性能。因此，我们只需要采样一小部分边来构建线图，这大大减少了操作线图所需的内存消耗。在 DBLP-ACM 数据集中，当 topk ≥ 200 时，DLNA 的变化很小（约为 |Vt|）。这表明我们可以在非常稀疏的相似矩阵上执行 Sinkhorn 操作，从而进一步减少内存占用。最后，我们观察到在实践中，仅需 3 到 5 次 Sinkhorn 迭代即可在稀疏版本的 S 上获得良好的性能。如图 6 所示，DLNA 在实现令人印象深刻的准确性的同时，消耗的时间比大多数基线方法更少。

image-20240903190346580

5.4 鲁棒性和不确定性分析

我们研究了 DLNA 在面对随机噪声时的表现，以展示其在建模不确定性方面的优势。我们在 DBLP 网络中随机插入边，扰动率从 0 增加到 25%，步长为 5%，同时保持 ACM 网络不受扰动。扰动率是指插入的边占原始边总数的比例。所有基线的 Hit@30 结果如图 7(a) 所示。可以观察到，当噪声不超过 7% 时，DLNA 具有最稳定的结果，当噪声比率超过 7% 时，DLNA 的表现与其他基线相当。我们进一步分析了图 7(b) 中的现象。在 DBLP 上 25% 扰动的情况下，我们根据 T = 1 计算每个测试锚节点 1 跳邻域内扰动边的比例，并按升序排列它们。对于扰动率在 [x,x+1)% 之间的节点，我们记录其平均 σ 并用蓝色误差条报告学习到的 σ 与扰动率之间的相关性。我们可以观察到，用来描述不确定性的 σ 可以反映扰动程度，随着噪声比率的增加而增加。当噪声比率超过 7% 时，对齐性能显著下降。这可能是因为当 σ 超过一定值时，输出不确定性显著增加，模型无法再准确对齐跨网络的相同节点，导致鲁棒性下降。然而，即使在高噪声比率的情况下，我们的方法仍然具有与基线相当的防御性能，下降率大致相同，如图 7(a) 所示。

6 结论

传统的基于嵌入的方法主要受限于节点的确定性表示，因此对结构差异非常敏感。为了解决这个问题，我们提出了一种新的基于分布学习的网络对齐框架，该框架采用了线图和在Wasserstein相似矩阵上执行的Sinkhorn操作。我们验证了该方法的有效性，并展示了其优于最新技术的卓越性能。