《Meta-SNA（简称）》阅读笔记

《Sinkhorn Distance Minimization for Adaptive Semi-Supervised Social Network Alignment》

《基于Sinkhorn距离最小化的自适应半监督社交网络对齐》

自认为这篇文章写的特别好，信息密度很大，实验做的也很全面，收获颇丰。建议看之前先看《Adversarial Learning for Weakly-Supervised Social Network Alignment》这篇19年的。

0 摘要

社交网络对齐，旨在跨不同社交平台链接相同的用户身份，是社交图挖掘中的一项基础任务。现有的大多数方法都是监督模型，需要大量人工标注的数据，考虑到社交平台之间的巨大差异，这在实际操作中不可行。最近，通过将社交网络之间的同构性整合作为从分布层面链接身份的补充，帮助缓解对样本级别标注的依赖。对抗学习被用于通过最小化两个社交分布之间的距离，学习一个共享的投影函数。然而，由于社交用户行为通常难以预测，同构假设可能并不总是成立，因此共享的投影函数不足以处理复杂的跨平台关系。此外，对抗学习存在训练不稳定和不确定性的问题，可能影响模型性能。本文提出了一种新的基于元学习(meta-learning-based)的社交网络对齐模型Meta-SNA，能够有效捕捉同构性以及每个身份的独特特征。我们的动机在于学习一个共享的元模型来保留全球的跨平台知识，并通过适配器为每个身份学习一个特定的投影函数。进一步引入Sinkhorn距离作为分布接近度的衡量标准，以解决对抗学习的局限性，它具有显式的最优解，并可以通过矩阵缩放算法高效计算。实验结果表明，我们在多个数据集上评估的模型表现优越，验证了Meta-SNA的优势。

关键词：元学习，半监督学习，社交网络对齐，社交网络分析。

1 引言

近年来，社交网络变得越来越流行且多样化。用户可以同时在多个平台注册，以享受各种类型的服务。例如，人们通常会注册LinkedIn寻找工作机会，同时在Instagram上分享日常生活的图片。在每个社交平台中，用户可以创建一个身份，通过关注其他兴趣相似的用户或发布博客来展示其独特的个人形象。跨多个社交平台对同一自然人的身份进行对齐，称为社交网络对齐（SNA）或用户身份链接（UIL）。社交网络对齐通过融合来自多个社交源的信息，有助于描绘用户的内在特征，这为许多实际应用提供了帮助，如好友推荐、信息扩散预测和网络动态分析。

大多数现有方法是监督式的，需要大量手动标注的身份对来完全训练一个二元分类器，以区分匹配的身份对和不匹配的身份对。然而，考虑到不同社交平台之间的隔离，收集足够的标注数据极为耗时且成本高昂。最近，一些半监督策略被提出，以利用未标注的实例来提供补充信息。与监督方法相比，半监督模型可以利用未标注的数据来帮助捕捉数据分布的内在形态，这在实际操作中更有可能实现社交网络对齐。

现有的半监督方法通常在样本对的层面上对齐身份，仍然面临样本级别标注稀缺的问题。最近，Li等人利用了社交网络之间的同构性信息作为无监督的补充。其动机在于，给定一组自然人，由于共享兴趣，他们在不同社交特征空间中的社交身份分布呈现相似结构。因此，社交网络对齐任务是在用户空间分布层面上进行的。研究问题进一步转化为学习一个理想的线性投影函数，以最小化两个社交分布之间的距离。Wasserstein距离被采用来衡量分布的接近度，并通过流行的对抗学习框架进行最小化。然而，基于对抗学习的解算器存在巨大的计算和统计限制，如计算负担、训练不稳定性、缺乏平滑性以及估计困难。因此，如果我们能够在避免棘手的对抗训练过程的同时，纳入分布层面的同构信息，将会更好。

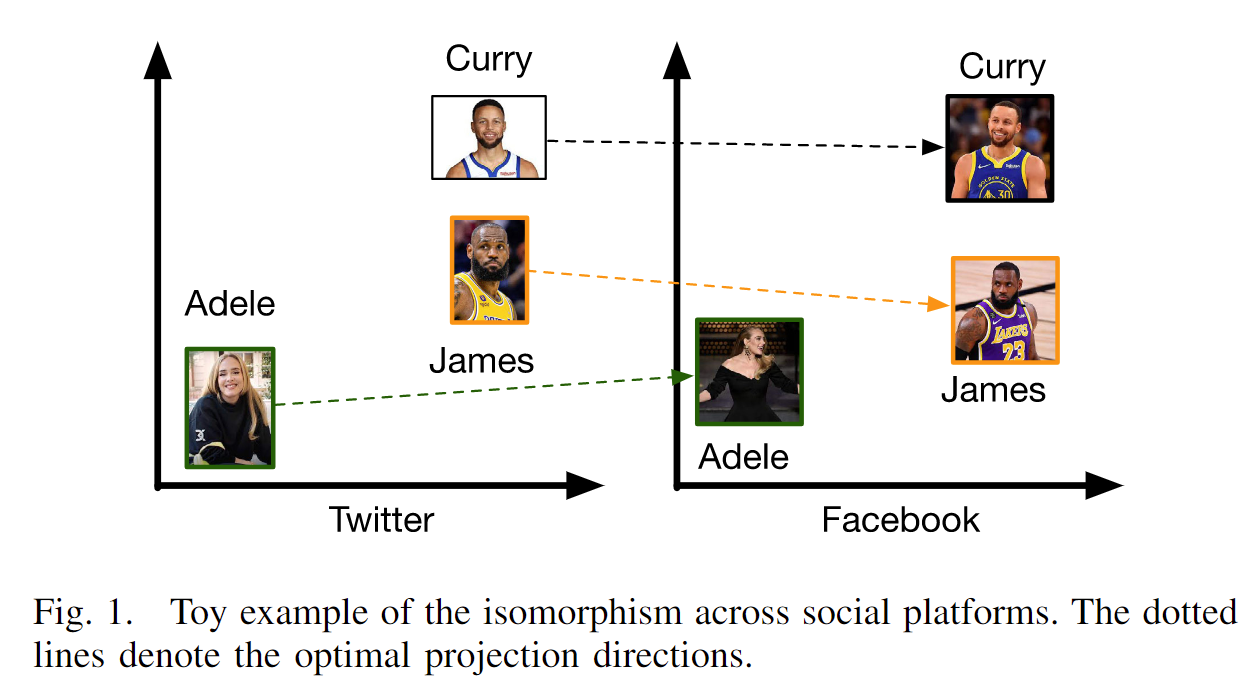
尽管同构增强模型在身份链接方面表现出色，但它们通常通过共享的线性投影函数来链接身份，这意味着同一社交网络中的不同身份被投影到相同的方向。然而，同构假设在一般情况下可能并不严格成立，因此全局共享的投影函数不是最佳解决方案。社交用户的行为通常是任意且不可预测的，因此不同的社交分布通常无法精确匹配。例如，如图1，虽然所有身份倾向于朝相似的方向移动，但由于不同社交网络分布的偏差，不同身份的最优变换略有不同。一个直接的策略是使用非线性投影来捕捉个性化的偏移。然而，非线性变换严重破坏了跨平台同构性，并进一步阻碍了链接性能。因此，如何在捕捉每个身份的具体或个性化特征的同时，保留全局同构信息，仍然不清楚。

在本文中，我们提出了一种基于元学习范式的新型社交网络对齐模型Meta-SNA。我们的动机是学习一个共享的投影函数来捕捉全局同构趋势，并通过适配器根据每个身份的独特属性微调共享投影函数。这种元学习范式能够为每个身份学习个性化的投影函数，同时不严重牺牲跨平台的同构性。所提出的Meta-SNA模型包括四个主要组件：身份建模、元投影、个性化适配器和分布距离估计器。具体来说，身份建模根据发布的微博和用户资料学习身份表示。元投影作为一种新的Householder反射实现，以确保严格的正交性，并将共享给所有身份。个性化适配器进一步调整元投影，以根据每个身份的特征学习独特的映射函数。对于分布距离估计器，不同于以前使用的地球移动者距离（EMD）和Wasserstein距离，本文引入了Sinkhorn距离作为分布接近度的衡量标准，这是一种基于最大熵的策略，可以顺利计算，无需生成器和判别器之间复杂的竞争。不同于生成对抗网络（GANs）中使用的生成器和判别器，我们这里只需要一个简单的神经网络来实现Sinkhorn距离，其计算本身就是一个优化问题。学习到的投影函数预期最小化两个社交分布之间的Sinkhorn距离，同时捕捉少量人工标注的指导，从而形成一个半监督学习框架。实证上，Meta-SNA在多个数据集上进行了评估，并在投影函数的质量和不同训练条件下的鲁棒性方面优于现有的基线模型，展示了我们提议的优势。

"Householder反射"是一种线性代数中的矩阵运算技术，常用于将向量反射到特定超平面上。它在数值计算和矩阵分解（例如QR分解）中有广泛的应用。

在社交网络对齐任务中，Householder反射实现是一种确保投影矩阵保持正交性（即矩阵的列向量彼此正交且单位长度）的技术。通过使用Householder反射，可以构造出严格正交的矩阵，用于投影不同社交网络中的身份数据到对齐的特征空间中。与其他方法相比，使用Householder反射可以提高计算的数值稳定性，并且在对齐过程中保持数据的几何结构不被破坏。

我们总结了主要贡献如下：

据我们所知，我们是第一个基于元学习范式为不同身份学习个性化投影函数的工作。
我们引入了Sinkhorn距离来衡量分布接近度，它拥有明确的最优解，帮助避免了棘手的对抗学习过程。
我们广泛地在五组数据集上评估了该提议。实验结果揭示了所提模型的优越性能。

2 相关工作

在本节中，我们将总结并介绍相关的研究工作。现有的社交网络对齐方法大致可分为监督、半监督和无监督方法。大多数现有方法是监督式的，通常将所研究的任务视为一个排名或分类问题，目的是定位具有最高链接概率的候选身份对。Man等人通过利用观察到的锚点链接作为监督信息来保持网络的主要结构规则。之后，学习了一个稳定的跨网络映射来链接相同的身份。Mu等人引入了“潜在用户空间”的新概念，并通过同时优化匹配/不匹配对和跨平台的内部关系约束来进行社交网络对齐。Zhang等人使用领域特定的先验知识作为指导，并应用概率分类器对一组广泛的社交网络档案进行链接，这是一个成本敏感的在线模型。Zhang等人引入了流行的图卷积网络（GCN），并联合捕捉本地和全局信息以进行社交网络对齐。Zhao等人提出了一个基于超图的模型UMAH，用于在一个统一的超图中建模社交结构和用户资料关系。Qiao等人则结合了用户网页浏览行为的最高层次特征表示来链接身份。

考虑到不同社交网络之间巨大的信息差异，收集足够的标注非常耗时且成本高昂。因此，提出了几种无监督的方法，自动定位已链接的身份对。Liu等人首先根据用户名在两个社交网络中的稀有性自动生成一组训练样本，然后使用这些样本训练二元分类器。Lacoste-Julien等人提出了一种贪心算法，根据启发式字符串相似性对用户属性进行对齐。POIS使用基于轨迹的属性特征来链接用户身份，首先计算用户身份之间的亲和分数，然后使用最大加权匹配方案找到最可能的匹配对。Li等人将社交网络中的所有用户视为一个整体，从用户空间分布层面进行社交网络对齐，并引入**地球移动者距离（EMD）**作为分布接近度的衡量标准来学习分布投影函数。虽然无监督方法消除了对标注样本的依赖，但它们通常由于缺乏指导性标注而表现较差。

最近，提出了几种半监督方法，旨在利用未标注数据来捕捉数据的内在分布，这些方法更有可能实现社交网络对齐。Korula等人设计了一种简单、局部且高效的算法，具有可证明的保证，并使用一小部分账户链接来识别网络中很大一部分用户。Zhang等人提出了一种基于能量的模型，考虑了局部和全局一致性，并开发了一种高效的次梯度算法，将原始的基于能量的目标函数转换为其对偶形式。Zhong等人提出了一个基于属性的模型和一个基于关系的模型，并通过联合训练框架相互增强以进行身份链接。JORA使用归纳图卷积网络（GCN）来联合学习用户表示和身份对齐模块。Li等人利用社交网络之间的同构性信息作为补充，在分布层面进行身份链接，并提出了三种基于对抗学习的模型来最小化两个社交分布之间的Wasserstein距离。他们进一步提出了一个基于多平台的社交身份链接模型，其中部分共享生成器和判别器，该模型也在对抗学习框架下定义。

分布最小化方法取得了有前景的对齐结果，但其对抗学习过程复杂且难以处理。本文旨在引入一种新的分布距离度量方法，既能通过最小化社交分布之间的距离来享受同构性的优势，又能提供更加稳定且明确的训练过程。

3 问题定义

在本节中，我们将正式定义所研究的问题。社交网络定义为：

N=\{U,E\}

其中，U = {u_1,u_2, \dots, u_{|N|}} 包含社交网络中的 |N| 个用户身份。每个身份都与一组社交数据相关，包括人口统计信息、用户行为或发布的文本数据。矩阵 E \in {0, 1}^{|N| \times |N|} 是无向社交关系图的邻接矩阵。所研究的问题正式定义如下：

定义 1（半监督社交网络对齐）：

两个输入网络定义为源网络 S = {U_s, E_s} 和目标网络 T = {U_t, E_t}。此外，部分匹配的身份对定义为 A = \{{(u_s, u_t)|u_s \in U_s, u_t \in U_t}\}，其中两个身份属于同一个自然人。我们的目标是找到其余的对齐身份对：

Y=\{(u_s,u_t)|u_s\in U_s,u_t\in U_t,(u_s,u_t)\notin A\}

社交网络的特征空间被视为离散分布：

\mathbb{P}^{S}=\sum_{n}p_{n}\delta_{e_{n}}

其中 p_n 是用户身份 u_n 的拓扑影响，e_n 是相应的特征向量，\delta 是狄拉克函数。

为什么使用狄拉克 delta 函数？

狄拉克 delta 函数 \delta(x - e_n) 的作用可以理解为在特定位置 e_n 上“激活”一个点，而在其他地方为零。换句话说，狄拉克 delta 函数用来捕捉在特征空间中某个用户身份的唯一性或确定性。

每个用户身份 u_n 都有一个唯一的特征向量 e_n，这个特征向量可以表示用户的行为、关系、人口统计数据等。

我们通过定义一个离散分布 P_S = \sum_n p_n \delta_{e_n} 来表示社交网络中所有用户身份的集合，其中 p_n 是用户 u_n 的权重或拓扑影响。

狄拉克 delta 函数 \delta_{e_n} 确保在特征空间中，只有在位置 e_n 上存在一个用户身份 u_n，而其他地方都没有用户身份。这使得特征向量和用户身份之间的关联非常明确。

为了从分布层面纳入同构信息，遵循之前的工作 [5]，研究问题可以转化为学习一个理想的投影函数，定义如下：

定义 2（社交网络对齐的投影函数学习）：

给定源分布 \mathbb{P}^{S}，目标分布 \mathbb{P}^T，以及注释集 A =\{ {(u_s, u_t)|u_s \in U_s, u_t \in U_t}\}，理想的投影函数 \text{Φ} 应满足以下两个条件：

\text{Φ} 应最小化投影源分布 \mathbb{P}^{\Phi(S)} 与目标分布 \mathbb{P}^{T} 之间的 Sinkhorn 距离，以纳入同构信息；
对于注释集A中匹配的身份对 (u_s, u_t)，\text{Φ} 应最小化投影源点 \text{Φ}(u_s) 与目标点 u_t 之间的距离，以纳入现有的标注。

在训练过程中，源身份 u_s 的投影点 \text{Φ}(u_s) 与目标身份候选 u_t 之间的距离可以被视为对齐的指标。较小的距离意味着两个身份更有可能是同一个人。遵循之前的工作 [13], [35]，假设两个输入网络是部分对齐的，即 |U_s| \neq |U_t|，这意味着在一个社交网络中有一部分身份在另一个网络中没有匹配。

4 方法论

在本节中，我们将介绍提出的Meta-SNA模型的主要组成部分的详细信息。

4.1 框架

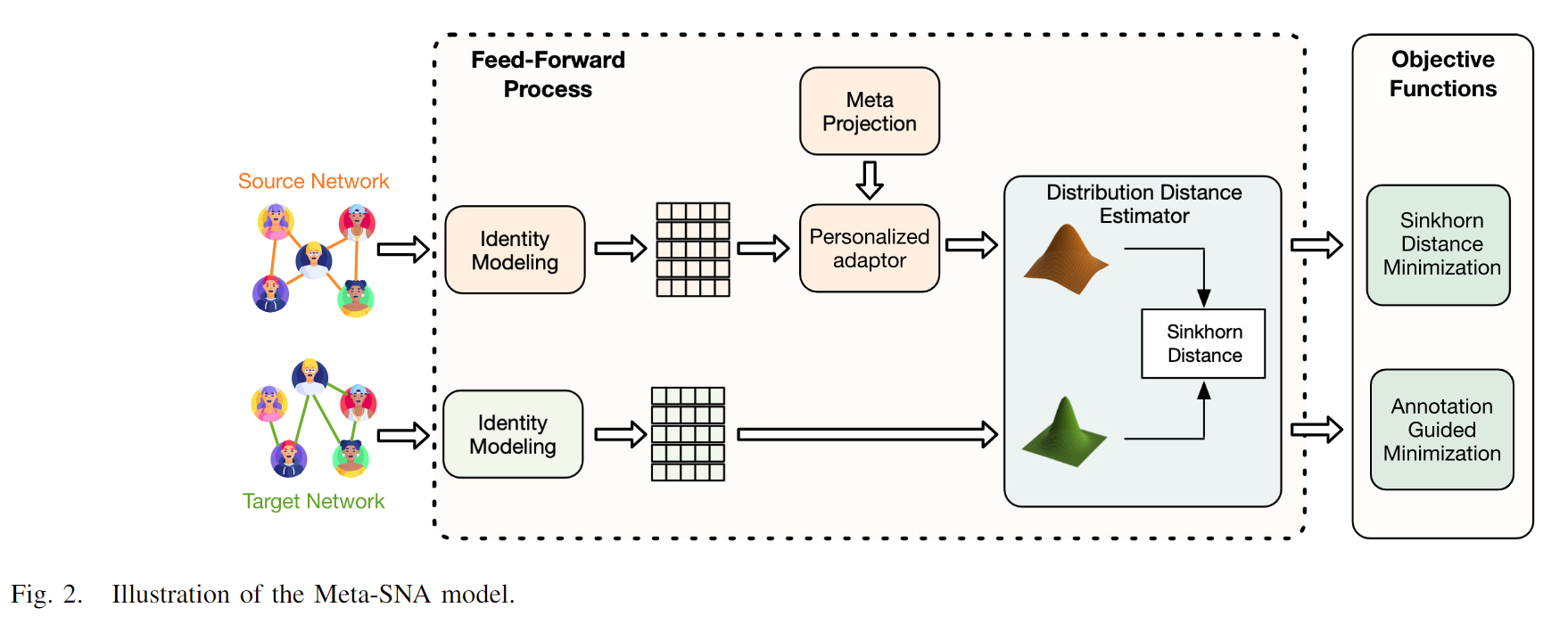
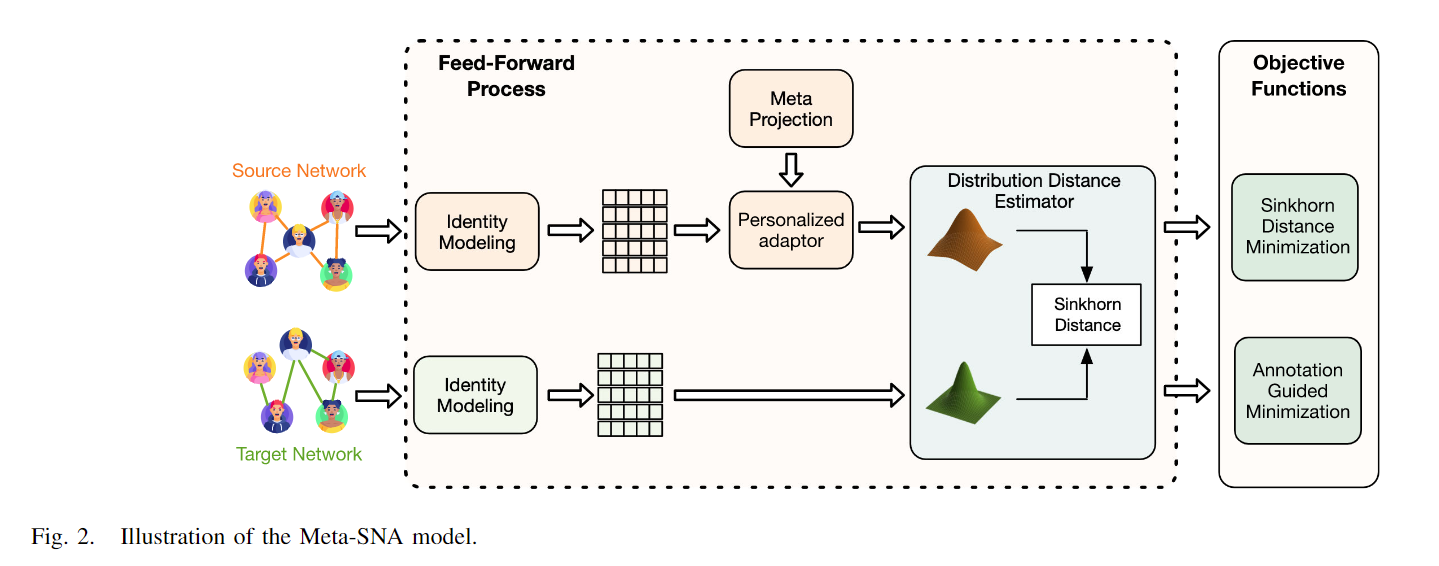
Meta-SNA模型的框架如图2所示。这里，我们以从源网络到目标网络的投影为例。

身份建模：给定两个输入的社交网络，身份建模模块首先将发布的博客、人口统计信息和社交关系嵌入到身份嵌入中。
元投影、个性化适配器：基于身份嵌入中的特征，个性化适配器微调共享的元投影，以为每个源身份学习唯一的投影函数，然后相应地将这些身份投影到目标空间中。
分布距离估计器：选择Sinkhorn距离作为分布度量。目标函数包括最小化Sinkhorn距离以捕捉同构信息，以及最小化引导少量注释的监督信号。源到目标的投影记作 G，而相反方向定义为 H。这两个方向都可以用于链接身份。

4.2 身份建模

身份建模旨在将用户的社交数据（例如，人口统计数据、发布的微博和社交关系）编码为低维嵌入。图3展示了身份建模模块的框架。

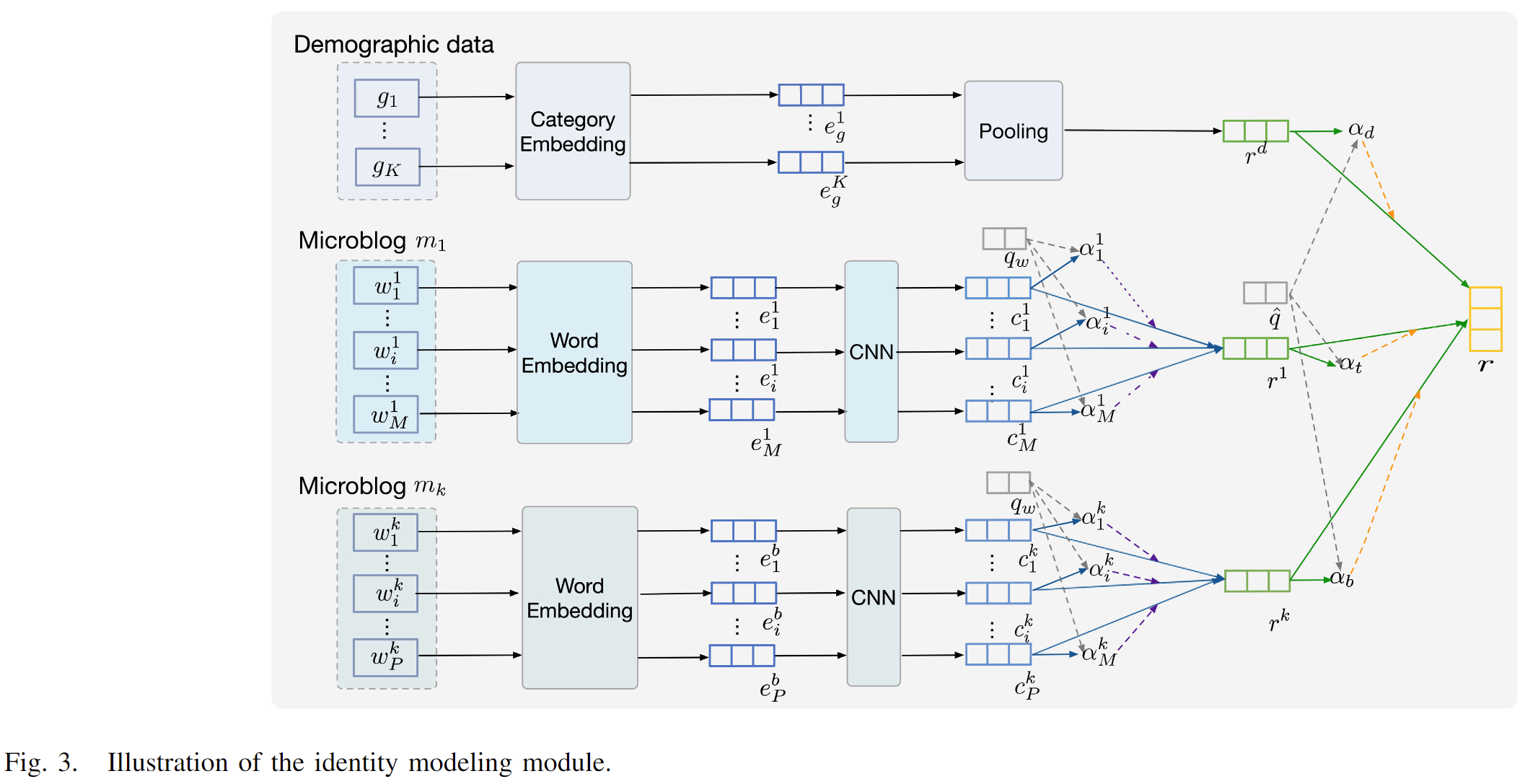
给定一个包含P个单词的微博 m_k （即 [w_{k1}, w_{k2}, \dots, w_{kP}]），我们首先基于预训练的词嵌入集合将输入的单词转换为相应的嵌入 [e_{k1}, e_{k2}, \dots, e_{kP}]。嵌入 e_{k_i} 保留了相关单词的丰富语义信息。然而，在微博中，一个词的实际含义受其最近邻居的影响。因此，引入了卷积神经网络（CNN）来学习上下文词表示 c_{k_i}，该表示能够在固定窗口大小内捕捉重要语义。

之后，引入自注意力机制来衡量不同单词的重要性。我们的动机在于，同一微博中的单词可能具有不同的信息量。例如，给定微博 "It is raining outside now"（“现在外面在下雨”），代表性单词“raining”比单词“it”和“is”更为重要。微博 m_k 中第 i 个单词的注意力得分形式化如下：

\begin{gathered} a_{i}^{k} =\sigma(q_w\cdot e_i^k+b_w) \\ \alpha_{i}^{k} =\frac{\exp(a_i^k)}{\sum_{i=1}^P\exp(a_i^k)} \end{gathered}

其中，q_w 和 b_w 是注意力网络的参数。学到的 \alpha^k_i 表示微博 m_k 中与其他单词相比，第 i 个单词的重要性。基于学到的注意力得分，微博的表示是上下文词嵌入的加权组合：

r^k=\sum_{j=1}^P\alpha_j^ke_j^k

除了微博之外，社交网络用户通常在个人页面中突出其人口统计信息。这些人口统计数据有助于描绘其社交身份的内在特征。我们收集了所有用户识别的人口统计标签，并将它们视为分类特征。每个标签对应于一个可学习的查找表中的嵌入。通过池化层，所有由单个用户发布的标签组合成一个单一向量 r^d。

基于微博的嵌入和社交身份的人口统计表示，我们还使用自注意力机制将它们结合在一起。我们的洞察是，不同的微博的重要性也是不同的。自注意力层与公式(1)中的相同，但参数不同。输出嵌入 r 将是社交身份的最终表示。

社交关系定义了不同社交身份之间的关联，这也有助于促进身份建模【37】。在这里，我们引入了图注意力网络【38】来学习拓扑增强的身份表示 \hat{r}。给定目标用户 u 和邻居 [u_{n1}, u_{n2}, \dots, u_{nZ}]，邻居 u_{ni} 对中心节点 u 的重要性定义为：

\alpha_{ui}=\frac{\exp(\sigma(a_s\cdot[r_u||r_{ni}]))}{\sum_{j=1}^Z\exp(\sigma(a_s\cdot[r_u||r_{nj}]))}

其中，|| 表示连接操作，a_s 是局部层次的注意力向量。输出的 \alpha_{ui} 表示邻居 u_{ni} 对中心用户 u 的重要性。之后，基于学到的注意力权重 \alpha_{ui} 对嵌入 r_{ui} 进行加权聚合，可以得到拓扑增强的身份表示 \hat{r}。

与原始表示 r 相比，学习到的 \hat{r} 编码了局部拓扑邻居，这可能提供更丰富的社交信息。然而，另一方面，引入邻居信息也增加了噪声的风险，因为社交用户的行为往往是不可预测的。因此，应该根据数据集和下游任务谨慎地选择这两种类型的表示。

4.3 元投影

如在介绍中所讨论的，同构性能够提供有价值的无监督信息，以提高链接性能。因此，我们提出了一种新的元投影，来捕捉共享的全局同构信号。遵循之前的工作【13】【14】，我们采用线性变换作为投影函数，因为这种简单形式的投影可以更好地保持原始分布结构，从而更好地保留同构信息。我们也尝试了非线性投影函数，但所有的非线性方法都表现较差，如第V-F2节所示。其可能的原因是非线性投影可能会严重扭曲原始分布，从而进一步破坏同构性。

给定源平台中的一个身份 u，元投影 G_{meta} 定义如下：

G_{meta}(u)=G_{meta}\times r_u

其中，G_{meta} \in \mathbb{R}^{d \times d} 是投影矩阵，r_u 是从身份建模模块中学到的嵌入。

之前的工作也展示了正交投影矩阵的优点【13】，其在理论上具有数值稳定性【34】【39】。如果 G_{meta} 是一个正交矩阵，则可以通过转置矩阵轻松从其投影版本中恢复源分布：G^T_{meta} G_{meta} = I，这确保了社交身份和自然人可以双向转换。此外，如果L2欧几里得距离被设定为地面距离，我们可以得到：

\frac{r_t^TG_{meta}r_s}{\|G_{meta}r_s\|\|r_t\|}=\frac{r_s^TG_{meta}^Tr_t}{\|r_s\|\|G_{meta}^Tr_t\|}

左侧部分计算了在网络 T 空间中 r_t 和 G_{meta} r_s 之间的距离，而右侧部分计算了在网络 S 空间中 r_s 和 G^T_{meta} r_t 之间的距离，它们是等价的。因此，使用正交投影矩阵时，地面距离的计算与所选择的社交空间无关。

常见的方法是向目标函数中添加额外的约束，强制映射矩阵为正交矩阵（即 G^T_{meta} G_{meta} = I）。然而，这些约束只能生成一个近似的正交矩阵，而不是严格的正交矩阵，这可能会妨碍SNA模型在捕捉无监督同构信息时的能力。在此，我们提出基于Householder矩阵【40】构建一个严格的正交映射函数，称为Householder投影（HP）。

Householder矩阵是线性代数和数值分析中广泛使用的矩阵。它是一个表示关于包含原点的超平面反射的方阵。给定单位向量 v \in \mathbb{R}^d，维度为 d \times d 的Householder矩阵 H_e 以 v 作为参数定义为 H_e(v)。该矩阵用于将向量和矩阵反射到包含原点且垂直于向量 v 的超平面上。给定输入向量 z，Householder矩阵通过反射关于与法向量 v 正交的超平面将 z 变换为 \hat{z}：

\hat{z}=H_e(v)z=z-2\langle z,v\rangle v

公式的最右边部分 2 \langle z, v \rangle v 可以拆解成几个部分来理解：

\langle z, v \rangle ：这个符号表示内积（或称为点积）。对于两个向量 z 和 v，它们的内积是一个标量，表示向量 z 和 v 在多维空间中的相似性。内积越大，两个向量的方向越相似。计算方法如下： \langle z,v\rangle=z_{1}v_{1}+z_{2}v_{2}+\cdots+z_{n}v_{n}

v ：这里是向量 v，它是Householder变换中定义的向量。

2 \langle z, v \rangle v ：这意味着先计算 z 和 v 的内积，然后将结果乘以2，再将结果与向量 v 相乘。这实际上是在 v 的方向上缩放，调整 z 在 v 方向的投影量。

整个表达式的含义是将向量 z 关于向量 v 所定义的超平面进行反射变换。这一变换调整了向量 z 在向量 v 方向上的分量，使得 z 被“反射”到这个超平面上。

左边为什么等于右边：

公式左边 H_e(v)z 表示对向量 z 进行 Householder 变换。这个符号代表一种反射操作，其中 H_e(v) 是 Householder 矩阵，v 是定义反射的单位向量。公式的作用是将向量 z 通过 v 所定义的超平面反射。

右边的表达式 z - 2 \langle z, v \rangle v 是对反射操作的具体计算。它的含义是：从向量 z 中减去在 v 方向上的两倍投影，达到反射的效果。

这个公式的左边和右边是等价的，右边的表达式给出了 Householder 变换的具体计算方式。这是因为 Householder 矩阵的一个主要特点是它可以通过这种简单的向量计算公式来表示反射的结果，而不需要直接使用矩阵乘法。

借助Householder矩阵，可以设计出一种新的HP作为元投影函数，该函数可确保严格的正交变换。HP通过连接一系列连续的Householder矩阵构造。更具体地，对于一组单位向量 V = {v_i}_{i=1}^{n}，其中 v_i \in \mathbb{R}^d，n 是一个正整数，我们定义HP如下：

在Householder矩阵的构造中，所选取的一组单位向量不需要相互正交。

HP(V)=\prod_{i=1}^nH_e(v_i)

我们可以从理论上证明以下定理：

定理1：HP的像是所有 n \times n 正交矩阵的集合，即 Image(HP) = O(n)，其中 O(n) 是n维正交群。

在数学中，像（image）通常指的是一个函数或变换作用在某个输入（通常是集合或元素）上，所得到的输出集合。

这里的 O(n) 是 n维正交群，它表示所有的 n \times n 正交矩阵。这个定理说明通过多个 Householder 矩阵的组合，可以生成所有的正交矩阵。

定理1的证明：

HP的像是所有 n \times n 正交矩阵的集合，记为 O(n)。我们首先证明HP的像是 O(n) 的一个子集。由于每个Householder矩阵都是正交的，因此多个Householder矩阵的乘积也是正交矩阵。因此，Image(HP) \subset O(n)。

接下来我们证明反过来也成立，即任何 n \times n 的正交矩阵 Q 都可以分解为 n 个Householder矩阵的乘积。

这可以通过使用Householder QR分解来证明【40】。这种分解允许我们使用n-1个Householder矩阵对任意全秩矩阵 W \in \mathbb{R}^{n \times n} 进行上三角化。具体来说，我们可以将 W 写成 W = QR，其中 Q 是正交矩阵，R 是上三角矩阵。通过对 R 的子矩阵逐步应用Householder反射，我们可以获得一系列正交矩阵，最终使 R 变为上三角矩阵，从而得到分解：

Q=H_nH_{n-1}\ldots H_1

其中每个 H_i 是一个与单位向量 v_i 相关的Householder矩阵：

H_e(v_{n-1})H_e(v_{n-2})\ldots H_e(v_1)W=R

这里，R \in \mathbb{R}^{n \times n} 是一个上三角矩阵，并且其前n-1个对角元素都是正的。当对正交矩阵 Q 进行Householder QR分解时，我们可以得到：

H_e(v_{n-1})H_e(v_{n-2})\ldots H_e(v_1)Q=R

这表明 R 是一个对角矩阵，其中前n-1个对角线元素等于 +1，最后一个对角线元素等于 +1 或 -1。如果 R 的最后一个对角线元素等于 +1，即 R = I，那么我们可以设 v_n = (0, 0, \dots, 0)^T \in \mathbb{R}^n，从而得到：

H_e(v_{n-1})H_e(v_{n-2})\ldots H_e(v_1)Q=I=H_e(v_n)

此外，我们还可以得到：

Q=H_e(v_1)H_e(v_2)\ldots H_e(v_n)

如果 R 的最后一个对角线元素等于 -1，我们可以设 v_n = (0, 0, \dots, 1)^T \in \mathbb{R}^n，从而得到相同的结论。

因此，HP的像是 O(n) 的一个子集，即 Image(HP) \subset O(n)，其中 O(n) 是n维正交群。每个Householder矩阵都是正交的，n个Householder矩阵的乘积也是正交矩阵。因此，Image(HP) \subset O(n)。此外，任何n \times n 的正交矩阵 Q 都可以分解为 n 个Householder矩阵的乘积。

使用HP函数作为元投影，给定源身份的表示 r，我们使用 V_s = {v_1, v_2, \dots, v_n} 作为元投影函数，定义为：

\hat{r}=G_{meta}(r)=HP(V_s)r=\prod_{i=1}^nH_e(v_i)r

其中 n = d 完全覆盖了所有 d \times d 的正交矩阵。根据定理1，HP在模型优化（如随机梯度下降）过程中确保了严格的正交性，这在理论上与其他方法相比具有吸引力。此外，HP的效率得到了保证。HP中的可学习参数数量为 d \times d，与传统映射矩阵相同。此外，通过采用公式(5)中的向量乘法代替矩阵-向量乘法，时间复杂度可以从 O(nd^2) 降低到 O(nd)。

疑问：在这个中，最终只能HP只能得到一个于r正交的矩阵，那怎么与网络中所有源身份r正交？

4.4 个性化适配器

元投影保留了全局同构信息，它将所有的身份向相同的方向移动。然而，同构性的基本假设可能并不总是成立，因为社交用户的行为通常是任意且不可预测的，因此不同的社交分布通常无法完全匹配。因此，个性化适配器旨在学习个性化的适配参数，以便根据特定身份调整元投影。我们的动机在于，将每个身份的独特信息整合进来，以校准共享的元投影，使其映射到个性化的方向。

基于此动机，我们提出了适配器网络，用于将共享的元投影定制为特定身份的个性化投影。该适配器被设计为能够有效地融合元投影中保留的全局同构信息，并结合单个身份的个性化兴趣。形式上，给定源身份 u_i，适配器学习到一个个性化的投影函数 G_{ui}，如下所示：

G_{ui}=\text{Adaptor}(G_{meta},\hat{r})

\hat{r} 是经过拓扑增强后的身份特征表示，通过整合邻居的关系信息，使得身份的表示更加丰富和全面。

元投影 G_{meta} 包括 n 个可学习的向量 {v_i}，表示第 i 个基向量。具体来说，对于第 i 个基向量 v_i，其参数适应如下：

\tilde{v_i}=v_i\diamond\phi_i

其中 \diamond 表示适配操作，\phi_i 表示适配参数。在这里，选择了 FiLM【41】作为适配操作，因为它在学习复杂的底层数据分布和选择性操控网络的特征方面具有强大的能力。适配参数 \phi_i 包括两组参数：缩放参数集 \gamma_i 和偏置参数 \beta_i。适配过程形式上定义为：

\tilde{v_i}=v_i\odot\gamma_i+\beta_i

适配参数是基于通过线性投影的拓扑增强表示 \hat{r} 学习到的：

\gamma_i=W_\gamma\hat{r},\quad\beta_i=W_\beta\hat{r}

在这里，我们选择拓扑增强的表示作为输入来学习适配参数，原因如下：首先，一些身份的社交数据可能较为稀缺，而它们的邻居可以提供补充信息。其次，连接身份的表示 \hat{r} 倾向于更加相似，因为它们通常共享相似的邻居，这与适配器的动机相符，即相似身份的投影方向也趋于相似。

通过适配器，每个身份 u_i 将从元投影中获得一个唯一的投影函数 G_{ui}。

为清晰起见，我们将个性化投影操作定义如下：

G_{\mathrm{ins}}(S)=[G_{u_1}(r_{u_1}),G_{u_2}(r_{u_2}),\ldots,G_{u_m}(r_{u_m})]

在这篇论文中，投影函数最初是基于HP（Householder Projection）生成的全局元投影。但是，通过个性化适配器，投影函数被进一步调整为每个身份的个性化投影。换句话说，虽然最初的投影函数是基于HP的，但最终学到的个性化投影函数在元投影的基础上通过个性化适配器进行了调整，不再是严格意义上的HP。

HP作为全局同构映射：

最初，元投影 G_{\text{meta}} 是通过HP（Householder Projection）生成的，这确保了全局同构映射的正交性和全局结构的保留。

HP利用多个Householder矩阵的组合，生成一个正交矩阵，用于捕捉不同社交网络中的相似全局结构。

个性化适配器的调整：

个性化适配器在元投影的基础上进行了个体化的调整，这种调整是基于每个身份的特征和拓扑增强表示（即考虑了每个身份在网络中的邻居信息）。

具体来说，适配器通过缩放参数 \gamma_i 和偏置参数 \beta_i 来调整元投影，从而生成个性化的投影函数 G_{ui}，使得每个身份的投影更加符合其个性化特征。

最终学到的投影函数：

经过个性化适配器调整后的投影函数 G_{ui} 不再是纯粹的HP，因为HP生成的是严格的正交矩阵，而个性化适配器引入了缩放和偏置，这破坏了正交性。

最终学到的投影函数是基于HP的全局投影，结合个性化适配器的调整，生成的个性化投影函数，因此它不再是标准的HP，而是一种基于HP的个性化投影函数。

4.5 Sinkhorn距离估计器

如介绍部分所述，投影函数 G_{\text{ins}} 应该能够最小化投影源分布 P^{G_{\text{ins}}(S)} 和目标分布 P^T 之间的距离。因其显式的训练过程而著名的 Sinkhorn 距离被引入作为分布接近性的度量【27】。

由于每个社交网络中的身份数量可能非常庞大，我们从每个网络中抽取相同大小的实例样本来形成训练批，即 S_b 和 T_b，且 |S_b| = |T_b| = m。具有更大拓扑影响力的身份有更高的采样概率。基于批量训练策略，我们的方案可以轻松应用于大规模数据集，确保其可扩展性和通用性。接下来，我们将计算样本分布 P^{G_{\text{ins}}(S_b)} 和 P^{T_b} 之间的 Sinkhorn 距离。同时，训练批中身份的拓扑重要性矩阵也被提取为 P_s 和 P_t。

首先，生成一个距离矩阵 M \in \mathbb{R}^{m \times m}，用于提供分布接近性计算的地面距离信息【42】。矩阵元素 M_{st} 是投影源点 G_{us}(u_s) 和目标身份 u_t 之间的地面距离：

M_{st}=d(G_{us}(u_s),u_t)

其中函数 d 用于计算对应特征向量之间的距离。由于训练批的大小通常非常小（例如128），处理这种成对的矩阵距离计算是可行且快速的。

Sinkhorn 距离在分布 P^{G_{\text{ins}}(S_b)} 和 P^{T_b} 之间的形式定义如下：

SD(P^{G_{\mathrm{ins}}(S_b)},P^{T_b})=\min_{O\in U_\alpha(P_s,P_t)}\langle O,M\rangle

在这个公式中，O表示传输矩阵，M 是一个地面距离矩阵，M_{ij} 表示源分布中的点 i 和目标分布中的点 j 之间的距离。通过内积 \langle O, M \rangle，你可以计算传输成本（即将源点 i 的质量传输到目标点 j 的成本）。

Tip. 正交性与地面距离无关

其中函数 \langle \cdot, \cdot \rangle 代表 Frobenius 内积：

Frobenius 内积：\langle A,B\rangle_F=\sum_{i=1}^m\sum_{j=1}^na_{ij}\cdot b_{ij}，这个定义就是遍历矩阵 A 和 B 的每个元素，然后把每个对应位置的元素相乘，最后把这些乘积求和。

下面的这种写法是用矩阵的迹（trace）来表示的。

矩阵的迹（trace）是指一个方阵主对角线元素的和。例如，给定一个矩阵 C：

C=\begin{pmatrix}c_{11}&&c_{12}\\c_{21}&&c_{22}\end{pmatrix}

它的迹是：\mathrm{tr}(C)=c_{11}+c_{22}

我们接下来考虑矩阵乘积 A^T B。假设 A 和 B 都是 m \times n 的矩阵，那么 A^T 是 n \times m 的矩阵，A^T B 是一个 n \times n 的方阵。

矩阵 A^T B 的主对角线元素是 A 和 B 的各个列向量的内积。也就是说，A^T B 的主对角线上的元素 (A^T B)_{ii} 是 A 的第 i 列和 B 的第 i 列的内积。

其实很容易理解，举两个矩阵纸上写一下就明白了。

\langle X,Y\rangle=tr(\overline{X\text{т}}Y).

U_{\alpha}(P_s, P_t) 是一个带有熵约束的传输多面体：

U_\alpha(P_s,P_t):=\{O\in\mathbb{R}_+^{m\times m}|O1_m=P_s,O^T1_m=P_t,h(O)\leq h(P_s)+h(P_t)-\alpha\}

其中 1_m 是全1向量，O 包含所有非负的 m \times m 矩阵，其列和分别等于 P_s 和 P_t，它可以概率性地解释为分布 P^{G_{\text{ins}}(S_b)} 和 P^{T_b} 的所有可能的联合概率。h 是定义在任何概率分布上的熵函数：

h(P_s)=-\sum_{i=1}^mp_i\log p_i

其中 \alpha 是一个超参数，用于控制模型的稳定性【27】。公式(16)中右侧的熵约束可以解释为 U_{\alpha}(P_s, P_t) 中的联合概率集，这些联合概率的相互信息足够小，以确保与 h(P_s) 和 h(P_t) 保持一致。

Sinkhorn距离计算算法

输入：

距离矩阵 M
拓扑重要性矩阵 P_s 和 P_t
超参数 \alpha
批大小 m
迭代次数 iter

参数：

自适应投影函数 G_{\text{ins}}

输出：

Sinkhorn距离 SD(P^{G_{\text{ins}}(S_b)}, P^{T_b})

步骤：

初始化常数：K := e^{-\alpha M}
初始化向量：v := 1_m / m
初始化迭代计数器：i = 0
开始迭代：当 i < iter 时：
1. u = r / Kv
2. v = c / K^T u
3. 更新 i = i + 1
计算 Sinkhorn 距离 SD(P^{G_{\text{ins}}(S_b)}, P^{T_b}) = u^T((K \odot M)v)
返回 SD(P^{G_{\text{ins}}(S_b)}, P^{T_b})

Sinkhorn 距离的目标是找到一个理想的传输多面体 O，以最小的努力将离散分布转化为另一个分布。传输努力是地面距离和分布之间传输概率的组合。

不同于流行的 Kullback-Leibler 散度或 Wasserstein 距离，Sinkhorn 距离引入了熵约束，用来限制在寻找低成本联合概率时的过度平滑性，从而得到更简洁的解决方案。Cuturi 等人【27】证明了公式(14) 在形式上具有最佳解，即：

O^*=\mathrm{diag}(u)K\mathrm{diag}(v)

其中 K := e^{-\lambda M}，u 和 v 是非负向量。参数 \lambda 是拉格朗日乘子，用于公式(16) 中的熵约束，每个 \alpha 对应于公式(14) 中的 \lambda。

使用矩阵缩放算法可以有效地计算 Sinkhorn 距离，如算法 1 所示。从该算法可以看出，这是基于迭代的计算过程，只需要矩阵-向量乘法。此外，Sinkhorn 距离的简单且显式的计算步骤确保了我们可以计算并反向传播 Sinkhorn 距离的梯度，进而更新投影函数 G_{\text{ins}} 中的参数。该投影函数将被更新以最小化计算出的 Sinkhorn 距离，如下所示：

\min L_{\mathrm{ds}}=SD(P^{G_{\mathrm{ins}}(S_b)},P^{T_b})(18)

4.6 最终目标函数

与此同时，我们也引入了一些注释来引导投影函数的学习。给定一个采样的训练批，我们假设存在一组源身份及其匹配的目标身份，记作 A_b \subset A。对于一个已对齐的身份对 (u_s, u_t) \in A_b，投影源点 G_{\text{ins}}(u_s) 应该接近其匹配的目标身份 u_t。因此，我们提出了以下目标函数来结合这些注释信息：

\min L_a=\frac{\lambda_a}{|A_b|}\sum_{(u_s,u_t)\in A_b}d(G_\text{ins}(u_s),u_t)(19)

其中 d 是地面距离函数，\lambda_a 是一个超参数，用于控制损失函数 L_a 的权重。公式(19) 结合了现有的注释信息来引导投影函数 G_{\text{ins}} 的学习过程。监督损失 (公式19) 和无监督损失 (公式18) 共同形成了一个统一的半监督学习框架。

总体来说，Meta-SNA 的最终目标函数是先前各目标的加权组合，如下所示：

\min L_G=L_{\mathrm{ds}}+L_a

其中，L_G 上标 G 表示从网络 S 到网络 T 的方向。目标从目标平台投影到源平台被表示为 H，这是映射 G 的相反方向。两个方向都可以用来进行身份链接。两个投影函数 G 和 H 以迭代的方式进行训练。具体来说，首先我们固定投影 H 并最小化损失 L_G 来学习投影 G，然后固定 G 来学习投影 H。计算出的损失可以通过深度学习框架反向传播来引导 G 和 H 的更新。

在模型训练过程结束后，投影函数 G 和 H 都可以用于身份链接。从实验结果来看，这两个投影的表现是相似的。因此，我们仅使用学习到的投影函数 G 来执行社交网络对齐任务。

5 实验

在本节中，我们将在多个真实世界的社交网络数据集上评估所提出的模型。我们首先介绍所使用的数据集、数据预处理方法以及基准方法。接下来，我们将展示并分析实验结果。随后，我们将进行学习行为分析和效率分析，以展示我们提议方法的优越性。最后，我们还将讨论模型在两个核心参数上的敏感性。

5.1 数据集

我们的提议方法在五个数据集上进行了评估，包括两对社交网络和三对学术合著网络。详细的统计数据如表I所示。

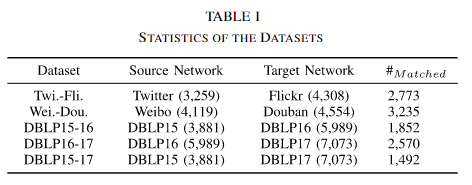
Twitter-Flickr：Twitter 和 Flickr 是两个流行的社交平台。此外，about.me 网站提供了一个中介平台，用户可以在上面链接不同社交网站上的身份，并展示其身份信息，这可以视为真实情况。我们从 Twitter 和 Flickr 中爬取了相同自然人的社交数据，获得了 3259 个 Twitter 身份和 4308 个 Flickr 身份，其中 2773 对是匹配的。此外，随机抽取了一组不匹配的身份，形成了部分共享数据集。
Weibo-Douban：新浪微博和豆瓣是中国的两个流行社交平台。豆瓣用户可以在其主页中展示他们的新浪微博账户，我们可以从中爬取这些链接信息作为真实情况。我们获得了 4119 个微博身份和 4554 个豆瓣身份，其中 3235 对是匹配的。同样，随机抽取了一组不匹配的身份，形成部分共享数据集。
DBLP：DBLP 是一个计算机科学文献数据库。我们选取了 DBLP 的公开数据集，包含 2015 年至 2017 年三年内的已发表论文及其作者。我们从中选择了三组合著网络。每年我们都选取 Yoshua Bengio 作为中心节点，并构建子合著网络，链接可以在三步内访问到中心节点的合著者。对于每一年的一个作者来说，其已发表文章被视为其属性，DBLP 数据集中的作者身份被视为真实情况。

5.2 数据预处理

对于每个社交网络，我们通过网络嵌入方法构建其低维特征空间。这里，我们选择了一种属性保留的网络嵌入模型 TADW【43】，将图的拓扑结构（例如好友或合著关系）和节点属性嵌入特征向量中。

对于 Twitter 用户，我们将其发布的推文视为节点属性。我们使用 NTLK【5】工具处理爬取的推文。对于 Flickr 数据集，我们收集了发布的图像、兴趣组以及每个用户的关注关系。

微博和豆瓣数据集的处理方式类似，只是用户属性略有不同（微博用户的兴趣标签和话题标签，豆瓣用户的兴趣标签和加入的群组）。

对于 DBLP 数据集，我们构建了2015年至2017年三年的合著网络。作者被视为节点，合著关系被视为边。对于一个网络中的某个作者，我们收集了他/她在这一年内已发表文章的标题和摘要，作为其属性。

5.3 基准方法

我们选择了一些先进的基准方法，包括半监督和监督模型。

MAH【18】：MAH 是一种结合网络结构信息的半监督模型，使用超图来建模高阶关系。对于一个社交网络中的目标用户，MAH 通过超图上的关系来挖掘潜在的用户链接信息。
COSNET【21】：COSNET 是一个基于能量的模型，考虑了局部和全局一致性，提出了一个能量模型来链接用户身份，并开发了一个有效的次梯度算法，将原始的基于能量的目标函数转换为其对偶形式。
IONE【22】：IONE 采用表示学习的方法来跨多个社交网络对齐用户，统一优化框架下同时解决了网络嵌入问题和社交网络对齐问题。
ULink【13】：ULink 引入了一个新的概念“潜在用户空间（Latent User Space）”，通过在不同平台上联合优化匹配/非匹配对和平台内关系约束来进行社交网络对齐。
UMAH【16】：UMAH 以超图作为基本模块，提出在统一的超图中建模社交结构和用户档案关系。
JORA【26】：JORA 使用归纳式图卷积网络（GCNs）联合学习用户表示和身份对齐模块。
CoLink【24】：CoLink 是一个弱监督模型，使用共同训练算法来处理基于属性和基于关系的模型，并在身份链接的共同训练框架中互相迭代加强。
SNNAu【25】：SNNAu 旨在学习一个投影函数，不仅最小化两个社交网络中用户身份分布之间的Wasserstein距离，还结合了可用的注释作为学习指导。SNNAu 是一种基于单向对抗学习的对齐模型。
SNNAo【25】：SNNAo 是 SNNAu 的扩展版本，加入了正交约束。

5.4 参数设置

对于所提出的模型，特征向量的维度设为100。最小训练批次的大小为256。在算法1中的超参数中，\alpha = 10，迭代次数（iter）为20。注释权重 \lambda_a 设为0.3，重构权重 \lambda_r 设为0.2。对于CoLink模型，我们使用SVM作为基于属性的模型，并从匹配的身份对中随机选择训练种子。ULink模型通过约束凸优化过程进行训练。对于SNNA模型，判别器在一次迭代中的训练次数 n_d 设为5，剪辑参数 c 设为0.01，注释权重 \lambda_c 设为0.2，重构权重 \lambda_r 设为0.3。其他基准模型中的参数按照原始文章中的设置。

评估指标：按照之前的工作【13】，命中精度（Hit-Precision）被选为评估指标：

h(x)=\frac{k-(hit(x)-1)}k

其中，hit(x) 是返回的前 k 名候选目标身份中匹配目标用户的排名位置。命中精度的计算方法是对匹配身份对的得分取平均值：(\sum_{i=0}^{m} h(x_i))/(m)，其中 m 是匹配对中的源身份数量。

5.5 实验结果

对于每个数据集，T_r 部分的对齐身份对被随机选择为训练注释，N_{te} 对被随机选择为测试样本。在这里，T_r 固定为10%，N_{te} 固定为300。我们重复该过程三次，并报告平均命中精度得分。

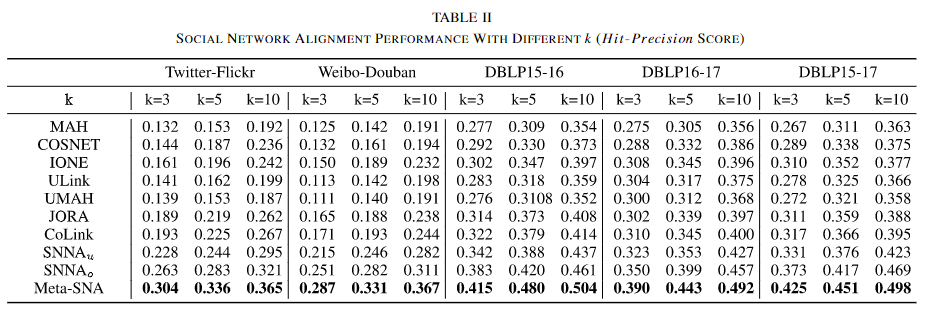
表2显示了在不同 k 设置下的命中精度得分。从结果可以看出，所有模型在共同作者网络上的表现优于社交网络，这可能是由于学术网络中的拓扑更加密集，以及节点属性的格式化更强。CoLink模型在所有基于样本级别的方法（如MAH、COSNET、IONE、CoLink、JORA、UMAH和ULink）中表现最好，因为它有效捕捉了节点属性与网络拓扑之间的高度非线性相关性。基于对抗学习的方法（SNNAu和SNNAo）在所有基线中表现最好，这表明引入分布级别的同构性有助于更好的身份对齐。SNNAo 比 SNNAu 高出约4%，证明了正交约束的有效性。我们的方法在所有数据集上的不同设置下持续表现最佳，并且在平均表现上超过了最好的基线模型 SNNAo。

实验结果证明了我们方法的优越性。

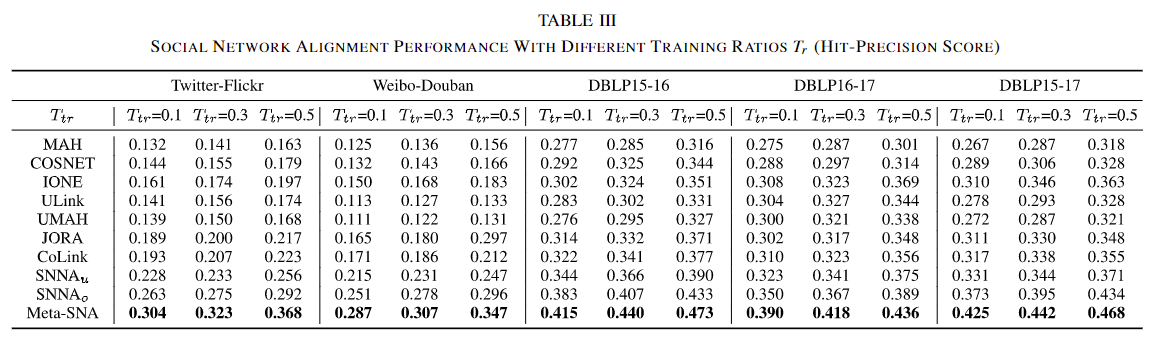
我们还进行了另一个实验，以研究在不同训练比 T_r 下社交网络对齐模型的表现。参数 k 固定为3，训练比 T_r 从0.1增加到0.5。表III展示了五个数据集上的命中精度得分。从实验结果中可以明显看出，随着训练比的增加，所有模型的表现都得到改善。这证明了注释可以提供与任务相关的指导信息，这也是无监督方法的局限性。

所提出的Meta-SNA模型在不同训练比下持续优于基线方法。随着注释数量的增加，Meta-SNA模型与其他模型之间的性能差距也在增加，这表明Meta-SNA的上限比其他模型更高。与Meta-SNA模型相比，基于对抗学习的方法表现出相对较低的性能，这证明了Sinkhorn距离的优越性。此外，所有基线都基于共享投影函数。显著的性能提升验证了所提出的元学习适配方法的有效性。

5.6 消融实验

在这里，我们从投影函数选择、用户建模、元投影和适配器的角度对Meta-SNA模型进行了消融研究。Hit-Precision计算中的参数k被固定为3，训练比例设置为0.1。消融研究是在四个数据集上进行的。

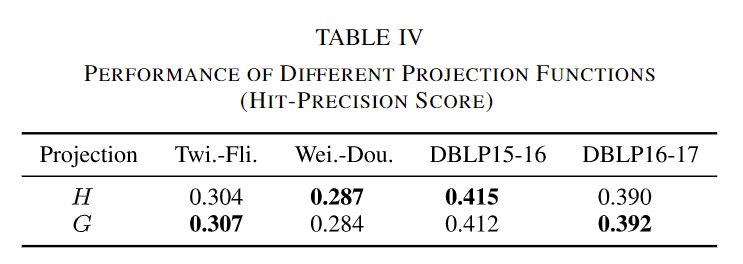
投影函数选择：从图2可以看出，Meta-SNA是一个双向学习模型，它包含两个投影函数（G将一个社交网络的分布投影到另一个社交网络的特征空间中，H执行相反方向的投影）。模型学习过程结束后，我们可以得到两个投影函数，它们都可以用于连接社交身份。我们在这里研究了不同投影函数的性能。表IV展示了实验结果。可以看到，两个投影函数几乎表现出相同的性能，这是合理的。首先，所提出的目标函数可以弥合两个投影之间的联系，这有助于在社交网络之间更好地捕捉同构性。其次，两个投影函数在统一的训练框架下学习，而不是分离训练。一个投影函数的梯度会影响另一个投影函数的学习过程，形成了一个整体。因此，两个投影函数G和H表现出相似的性能，任何一个都可以用于执行社交网络对齐。
线性投影与非线性投影：以前的工作表明，非线性投影往往会破坏同构信息。在这里，我们进行了消融研究，以进一步调查这一观察。我们结合了几种流行的非线性激活函数（tanh, sigmoid, relu, gelu）与原始投影形成非线性投影函数。对于线性投影，我们选择了标准线性变换和HP（HP-linear）作为对比方法。表V展示了实验结果。我们得出两个结论：
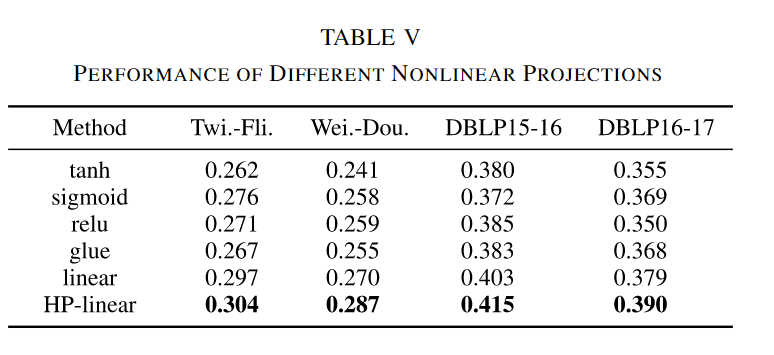
1. 与线性投影相比，非线性投影的性能显著下降，这与之前的观察一致，表明非线性变换会破坏跨平台同构性。
2. 与标准线性投影相比，所提出的HP线性投影进一步提高了对齐性能，表现提升了近1.5%，这表明正交变换有助于更好地保持同构性信息。
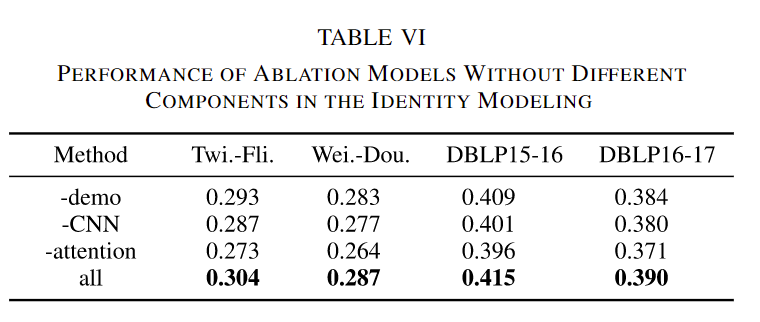
身份建模：这里，我们研究了身份建模模块中不同组件的重要性。设计了三个消融模型：
1. -demo：从Meta-SNA模型中移除人口统计数据。
2. -CNN：从Meta-SNA模型中移除CNN模块。
3. -attention：从Meta-SNA模型中移除注意力模块。

实验结果如表VI所示。可以清楚地看到，移除任何组件后，模型性能一致下降。细粒度分析表明，-demo显示出最小的性能下降，这揭示了文本数据可能在SNA场景中比人口统计数据更重要。-CNN稍微优于-attention，这表明全局注意力机制可能优于CNN中使用的局部过滤。

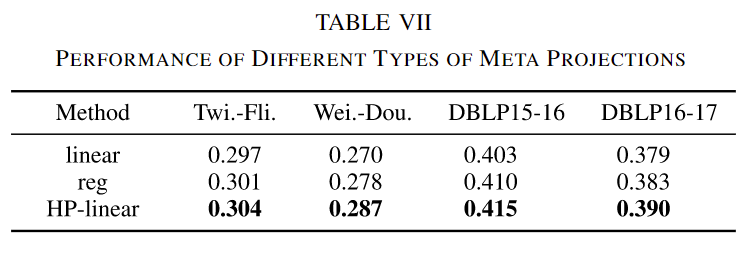
元投影：线性和非线性投影之间的比较已经在前面的部分中讨论过。我们在这里专注于正交变换的实现。提出了一种消融模型reg，使用原始线性投影，并在训练损失中添加新的正则化以确保正交性。表VII展示了实验结果。模型性能随着正交性变得更加严格而一致地提高。这与之前的工作一致，表明正交投影矩阵由于其数值稳定性而具有吸引力。reg模型只能确保投影接近正交性，而我们的方案在理论上可以确保正交投影，因此我们的方法达到了最佳性能。
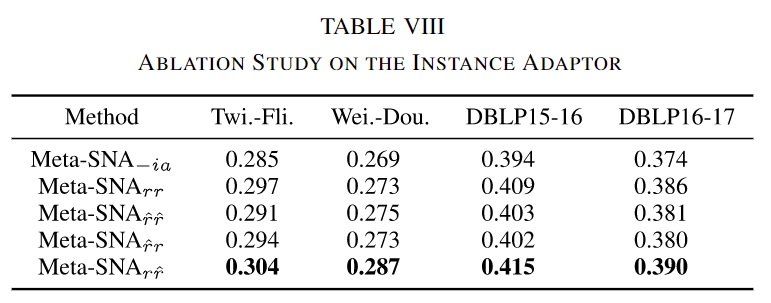
实例适配器：我们设计了以下四个消融模型来研究实例适配器中不同组件的有效性。
1. Meta-SNA-ia：移除实例适配器，并使用元投影作为最终的投影函数。
2. Meta-SNA-r：使用表示r作为身份嵌入，并使用输入向量生成适配参数。
3. Meta-SNA-\hat{r}：使用拓扑增强表示\hat{r}作为身份嵌入，并使用输入向量生成适配参数。
4. Meta-SNA-r\hat{r}：同时使用r和\hat{r}生成适配参数。

表VIII展示了实验结果。

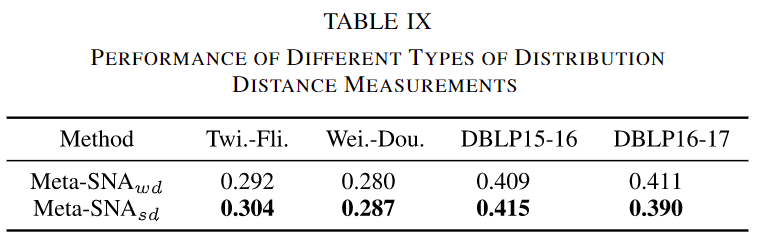
分布距离度量：为了验证Sinkhorn距离的有效性，我们将Wasserstein距离作为基线Meta-SNA_wd，并使用对抗学习来最小化Wasserstein距离。基于表IX中的实验结果，可以清楚地看到基于Sinkhorn距离的方法Meta-SNA_sd优于基于Wasserstein距离的方法，这验证了引入的Sinkhorn距离度量的有效性。

5.7 学习行为分析

为了证明Sinkhorn距离与基于对抗学习方法的优越性，我们展示并分析了Meta-SNA在使用Wasserstein距离（WD）和Sinkhorn距离（SD）的情况下的训练轨迹，它们在DBLP15-16数据集上进行了评估，设置为k=5。在模型学习过程中，每经过10000个训练批次，将保存一个检查点模型。每个检查点模型计算的分布距离（Wasserstein距离和Sinkhorn距离）与对应的Hit-Precision得分一起被记录下来。请注意，我们将近似分布距离重新缩放到0到10的范围，以便于清晰表示。

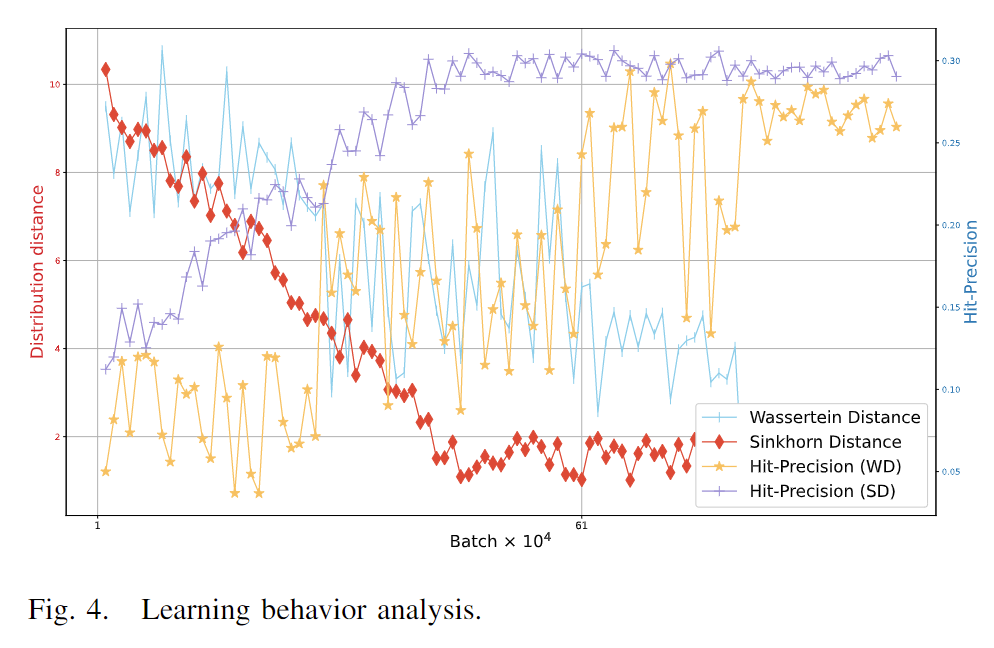
图4显示了两个模型的训练轨迹。可以看到，模型的学习过程波动较大，难以收敛。而Sinkhorn距离（SD）的训练轨迹更加平滑和一致，这表明Sinkhorn距离最小化在数值上比Wasserstein距离更稳定。SD需要较少的训练批次数来达到最优解，而WD需要更多的训练批次来通过生成器和判别器之间的竞争寻求纳什平衡。从图4中，我们还可以观察到，随着Sinkhorn距离的减小，Hit-Precision得分上升，这表明较小的Sinkhorn距离有助于更好的对齐性能，且同构确实有助于提高社交网络对齐的性能。此外，随着训练批次数的增加，估计的Sinkhorn距离减少，这证明我们的模型能够有效降低两个社交分布之间的Sinkhorn距离。

5.8 参数敏感性研究

最后，我们研究了 Meta-SNA 模型对两个核心参数的性能敏感性：标注权重 \lambda_a 和 Householder 反射次数 n。训练比例 T_r 设置为 10%，k 固定为 5。这两个参数的变化范围从 0.1 到 0.5，并且在四个数据集上记录了不同设置下的 Hit-Precision 分数，如图 5(a) 所示。

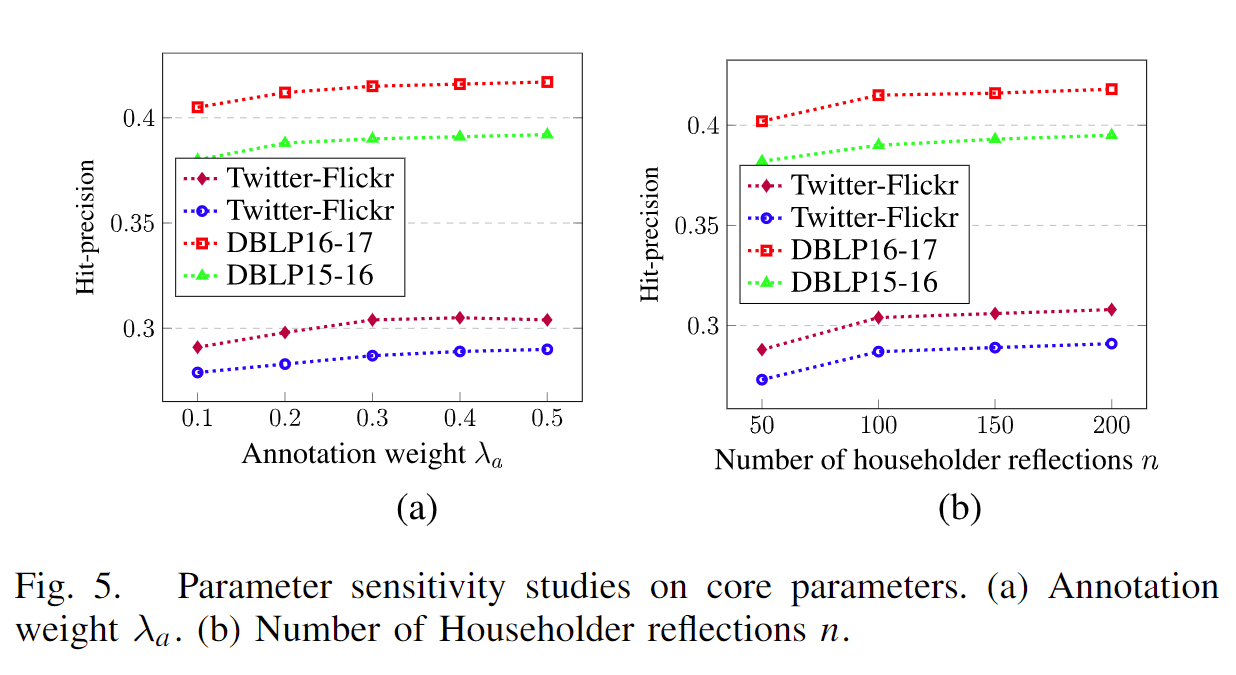
从左侧图可以看出，随着 \lambda_a 的增加，所有数据集的性能最初上升，然后保持稳定。这意味着标注权重 \lambda_a 的增加在初期有助于更好的对齐性能。当可用的标注充分利用时，可能需要更多的标注来进一步提高性能。

从右侧图可以看出，随着 n 的增加，模型性能最初显著上升，然后略有上升。这是合理的，因为更多的 Householder 反射意味着投影可以在更大的旋转空间中进行，这在初期有助于归纳性能。当 n 等于或大于身份嵌入的维度 d = 100 时，HP 达到了其表现力的峰值，因此无法带来更多的益处。

5.9 模型效率分析

在本节中，我们分析了所提模型的效率。我们选择对抗学习（adversarial-learning）为基础的模型（SNNA）作为对比方法。此外，我们将Sinkhorn距离替换为Wasserstein距离，称为\mathrm{Meta-SNA}_{wd}。本文报告的运行时间是在Ubuntu 64位Linux工作站上完成的，配置为4核Intel Core(TM) i7-6700 2.40 GHz处理器和128GB内存，深度学习模型在NVIDIA Tesla P100 GPU上运行。选择了两对社交网络数据集和两对学术网络数据集作为评估数据集。

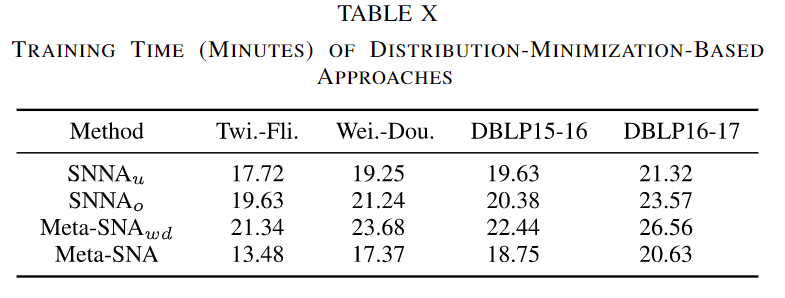
表X展示了不同社交网络对齐楼型的运行时间。运行时间与数据集大小存在明确的线性关系。SNNA_o 的运行时间比SNNA_u更长，因为SNNA_o模型在保证所学习的投影矩阵是正交的过程中增加了额外的计算量。Meta-SNA_{u:d}的运行时间比SNNA模型罗慢，这是由于来自适配器的额外计算成本所致。相比所提出的Meta-SNA横型，对抗学习横型的计算时间更长，因为它们需要通过生成器与判别器之间的竞争来寻求纳什均衡，而Meta-SNA可以通过矩阵缩放算法高效地计算。此外，Meta-SNA楼型仍然以更少的训练时间优于对抗学习楼型，证明了Sinkhorn距离的优越性。

6 结论

在本文中，我们研究了半监督社交网络对齐的任务。Sinkhorn 距离被引入作为度量分布接近性的手段，以应对不可处理的对抗学习过程的挑战。我们将该问题转化为学习理想的投影函数，这不仅可以最小化两个社交分布之间的 Sinkhorn 距离以引入同构信息，还结合了少量的注释以提供更强的指导。此外，我们提出为每个身份学习个性化的投影函数，以同时捕捉全局同构性和单个身份的独特特征。我们提出了一种基于元学习的模型 Meta-SNA 来解决上述问题。我们的提议在五个现实生活数据集上进行了广泛的评估。实验结果表明，Meta-SNA 模型在更稳定的训练过程中实现了最佳的对齐性能。

尽管提出的 Meta-SNA 模型具有潜力并表现出良好的性能，但它仍存在以下三个限制：

1）社交数据可能未得到充分利用。例如，微博中的话题标签在语义上与普通单词不同，应该单独处理；

2）目前我们的模型无法处理跨多个平台的身份链接问题【6】，这为元学习框架带来了新的挑战；

3）在工业中，在线学习的身份链接模型更有价值【1】，但遗憾的是我们的模型只能支持离线训练。这将是未来有前途的工作方向。