RW与RWR的Python简单实现

写在前面

关于入门资料，随机游走Random Walk(RW)的中文资料相对多一些，推荐 点击跳转

想找一下重启随机游走Random Walk with Restart(RWR)算法的介绍，发现中文的blog全是互相抄的，讲的不是很清楚。外网找到一篇还不错的 点击跳转

学完以后想看一下直观的效果跑一下代码，写了一个简单的python小程序结合tensorboard图表(别问为什么是tensorboard博主没学过可视化只会用这个)看看效果，这里分享出来

random_walk.py

import torch
import numpy as np
from torch.utils.tensorboard import SummaryWriter
import random

# 初始化TensorBoard
writer = SummaryWriter()


def create_graph():
    # 创建一个有十个节点的图的邻接矩阵
    adjacency_matrix = torch.tensor([
        [0, 1, 0, 1, 0, 0, 0, 0, 0, 0],
        [1, 0, 1, 0, 1, 0, 0, 0, 0, 0],
        [0, 1, 0, 0, 0, 1, 0, 0, 0, 0],
        [1, 0, 0, 0, 1, 0, 1, 0, 0, 0],
        [0, 1, 0, 1, 0, 1, 0, 1, 0, 0],
        [0, 0, 1, 0, 1, 0, 0, 0, 1, 0],
        [0, 0, 0, 1, 0, 0, 0, 0, 0, 1],
        [0, 0, 0, 0, 1, 0, 0, 0, 1, 0],
        [0, 0, 0, 0, 0, 1, 0, 1, 0, 1],
        [0, 0, 0, 0, 0, 0, 1, 0, 1, 0]
    ], dtype=torch.float32)
    return adjacency_matrix


# 使用Floyd算法计算矩阵中每个点到其他点的最短路径
def floyd(adjacency_matrix):
    num_nodes = adjacency_matrix.shape[0]
    # 将没有直接连接的节点的距离设置为无穷大
    distance = adjacency_matrix.clone()
    distance[distance == 0] = float('inf')
    # 将对角线设置为0
    distance[torch.arange(num_nodes), torch.arange(num_nodes)] = 0

    for k in range(num_nodes):
        for i in range(num_nodes):
            for j in range(num_nodes):
                if distance[i, j] > distance[i, k] + distance[k, j]:
                    distance[i, j] = distance[i, k] + distance[k, j]

    return distance


def random_walk(adjacency_matrix, start_node, max_steps=10):
    num_nodes = adjacency_matrix.shape[0]
    current_node = start_node
    steps = [current_node]

    for _ in range(max_steps):
        neighbors = [i for i in range(num_nodes) if adjacency_matrix[current_node, i] > 0]
        if not neighbors:
            break
        current_node = random.choice(neighbors)
        steps.append(current_node)
    return steps


adjacency_matrix = create_graph()

for i in range(100):
    start_node = i % 10  # 从不同的节点开始游走
    steps = random_walk(adjacency_matrix, start_node, 30)
    walk_tag = f'RW_StartNode_{start_node}/Walk_{i/10}'

    for step_idx, node in enumerate(steps):
        # 使用不同的标签来区分每次游走
        writer.add_scalar(walk_tag, node, step_idx)


writer.close()

# 使用Floyd算法计算矩阵中每个点到其他点的最短路径
distance = floyd(adjacency_matrix)
print(distance.numpy())

random_walk_with_restart.py

import torch
import numpy
from torch.utils.tensorboard import SummaryWriter
import random

# 初始化TensorBoard
writer = SummaryWriter()


def create_graph():
    # 创建一个有十个节点的图的邻接矩阵
    adjacency_matrix = torch.tensor([
        [0, 1, 0, 1, 0, 0, 0, 0, 0, 0],
        [1, 0, 1, 0, 1, 0, 0, 0, 0, 0],
        [0, 1, 0, 0, 0, 1, 0, 0, 0, 0],
        [1, 0, 0, 0, 1, 0, 1, 0, 0, 0],
        [0, 1, 0, 1, 0, 1, 0, 1, 0, 0],
        [0, 0, 1, 0, 1, 0, 0, 0, 1, 0],
        [0, 0, 0, 1, 0, 0, 0, 0, 0, 1],
        [0, 0, 0, 0, 1, 0, 0, 0, 1, 0],
        [0, 0, 0, 0, 0, 1, 0, 1, 0, 1],
        [0, 0, 0, 0, 0, 0, 1, 0, 1, 0]
    ], dtype=torch.float32)
    return adjacency_matrix


# 使用Floyd算法计算矩阵中每个点到其他点的最短路径
def floyd(adjacency_matrix):
    num_nodes = adjacency_matrix.shape[0]
    # 将没有直接连接的节点的距离设置为无穷大
    distance = adjacency_matrix.clone()
    distance[distance == 0] = float('inf')
    # 将对角线设置为0
    distance[torch.arange(num_nodes), torch.arange(num_nodes)] = 0

    for k in range(num_nodes):
        for i in range(num_nodes):
            for j in range(num_nodes):
                if distance[i, j] > distance[i, k] + distance[k, j]:
                    distance[i, j] = distance[i, k] + distance[k, j]

    return distance


def random_walk_with_restart(adjacency_matrix, start_node, max_steps, restart_prob):
    """
    @:param adjacency_matrix: 邻接矩阵
    @:param start_node: 开始节点
    @:param max_steps: 最大步数
    @:param restart_prob: 重启概率
    """
    num_nodes = adjacency_matrix.shape[0]
    current_node = start_node
    steps = [current_node]

    for _ in range(max_steps):
        # 以概率restart_prob重启
        if random.random() < restart_prob:
            current_node = start_node
            steps.append(current_node)
            continue

        neighbors = [i for i in range(num_nodes) if adjacency_matrix[current_node, i] > 0]
        if not neighbors:
            break
        current_node = random.choice(neighbors)
        steps.append(current_node)

    return steps


adjacency_matrix = create_graph()

for i in range(100):
    start_node = i % 10  # 从不同的节点开始游走
    steps = random_walk_with_restart(adjacency_matrix, start_node, 30, 0.15)
    walk_tag = f'RWR_StartNode_{start_node}/Walk_{i / 10}'

    for step_idx, node in enumerate(steps):
        # 使用不同的标签来区分每次游走
        writer.add_scalar(walk_tag, node, step_idx)

writer.close()

# 使用Floyd算法计算矩阵中每个点到其他点的最短路径
distance = floyd(adjacency_matrix)
print(distance.numpy())

运行结果分析

首先我通过控制台输出了10个节点构成的图中，每个点到其他点的最短路径，我在这里认为两个点之间的路径越短它们的联系就越紧密

C:\Users\67093\.conda\envs\pytorch\python.exe D:\Python程序\RWR\random_walk_with_restart.py 
[[0. 1. 2. 1. 2. 3. 2. 3. 4. 3.]
 [1. 0. 1. 2. 1. 2. 3. 2. 3. 4.]
 [2. 1. 0. 3. 2. 1. 4. 3. 2. 3.]
 [1. 2. 3. 0. 1. 2. 1. 2. 3. 2.]
 [2. 1. 2. 1. 0. 1. 2. 1. 2. 3.]
 [3. 2. 1. 2. 1. 0. 3. 2. 1. 2.]
 [2. 3. 4. 1. 2. 3. 0. 3. 2. 1.]
 [3. 2. 3. 2. 1. 2. 3. 0. 1. 2.]
 [4. 3. 2. 3. 2. 1. 2. 1. 0. 1.]
 [3. 4. 3. 2. 3. 2. 1. 2. 1. 0.]]

进程已结束,退出代码0

以0节点为例，它与其余各点的距离为[0. 1. 2. 1. 2. 3. 2. 3. 4. 3.]，即1、3节点距离0节点最紧凑，其次是2、4、6节点...

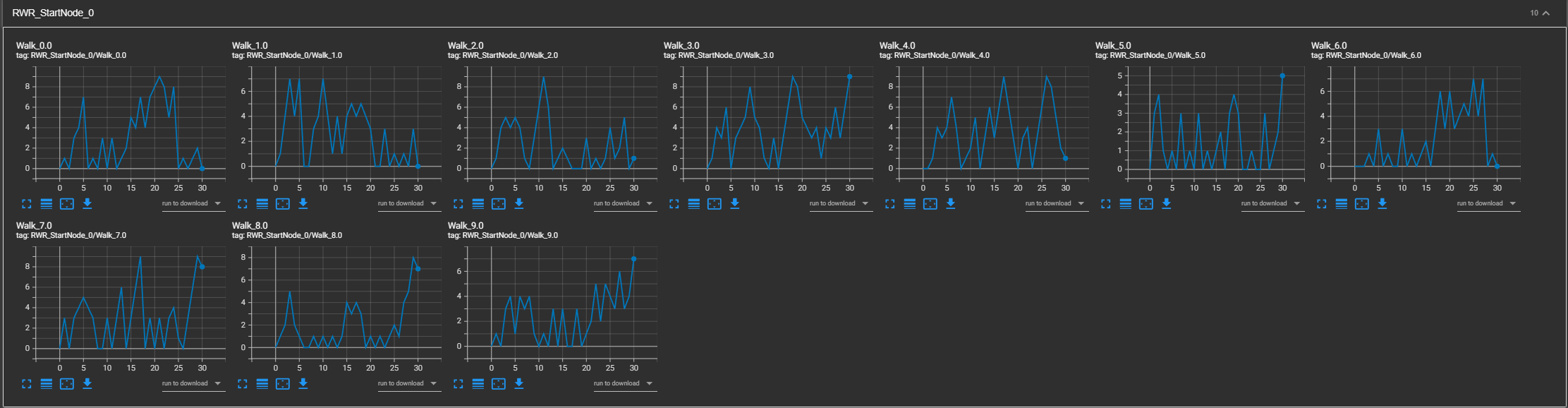
然后我们观察tensorboard的结果，他展示了从十个节点分别出发进行30步随机游走以及重启随机游走，该节点的游走过程以及最终位置

这里我们以从0节点出发进行的十次30步RW/RWR实验为例进行分析：

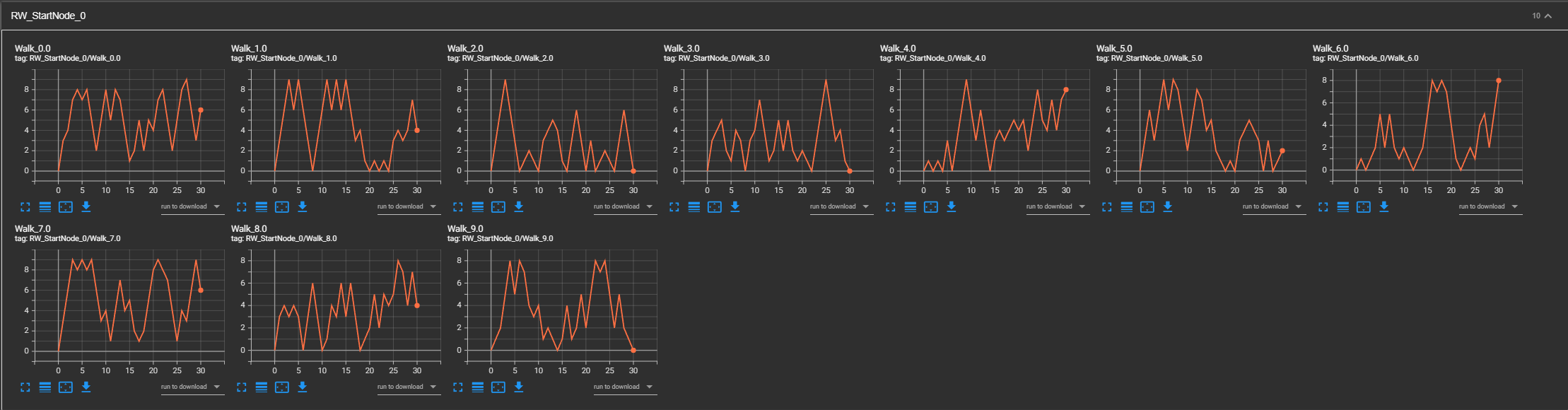
上面是RW，下面是RWR

在RW实验中，我们发现最终停留点的分布较为分散，没有明显的聚集现象。随着实验次数的增加，这一分布趋向于高斯分布，且最终的分散程度与实验次数的平方根成正比。这一观察符合随机游走的理论预期，即游走者在无偏随机游走过程中的位置分布逐渐趋于正态分布，反映了在无方向性约束下的随机性特征

与RW不同，RWR实验结果展现了一种不同的现象：最终停留节点的占比与起始节点（在本例中为0号节点）与其他节点的距离紧密程度成正比。这意味着，与起始节点距离较近的节点更有可能成为重启随机游走的最终停留点。这一结果揭示了RWR过程中的偏好性，即游走者在游走过程中具有返回起始点或其附近节点的倾向，进而增强了与起始节点紧密相连节点的访问概率